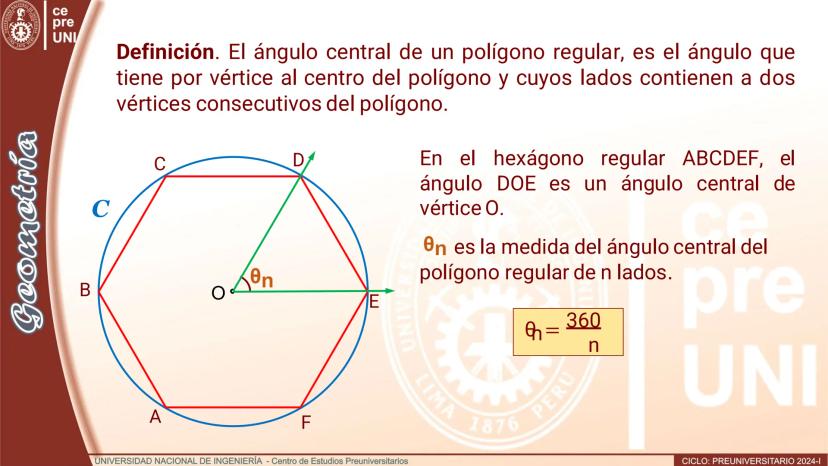
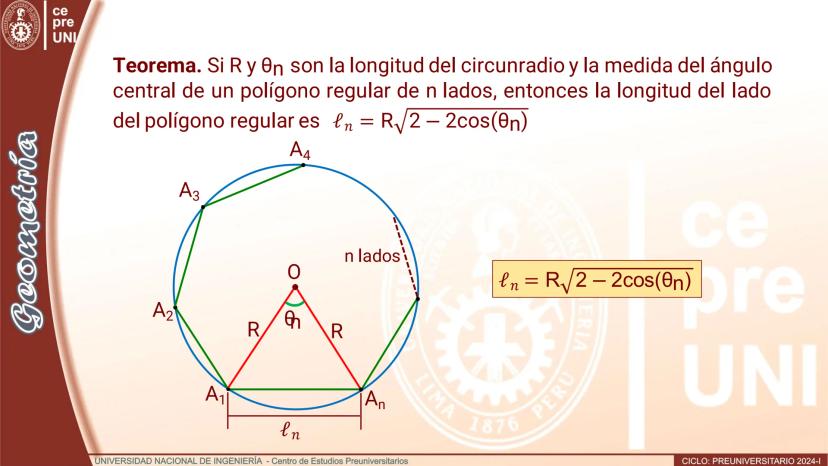
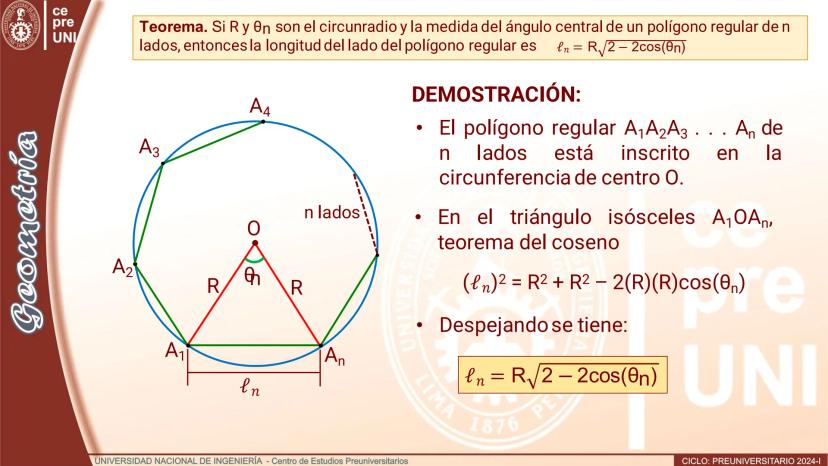
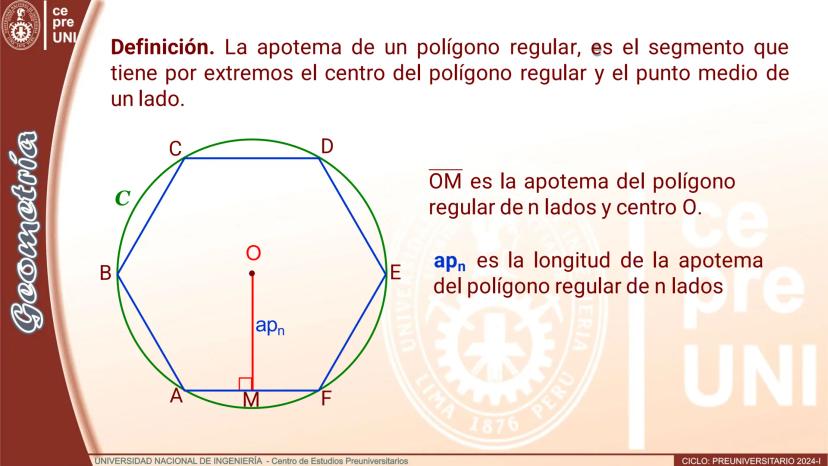
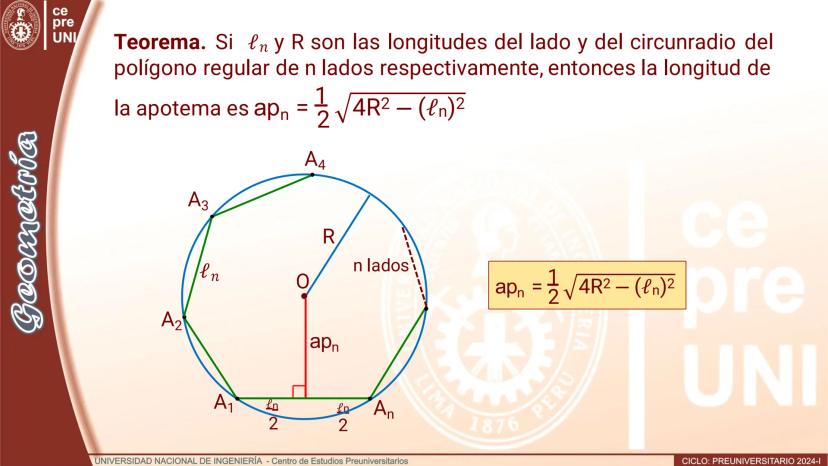
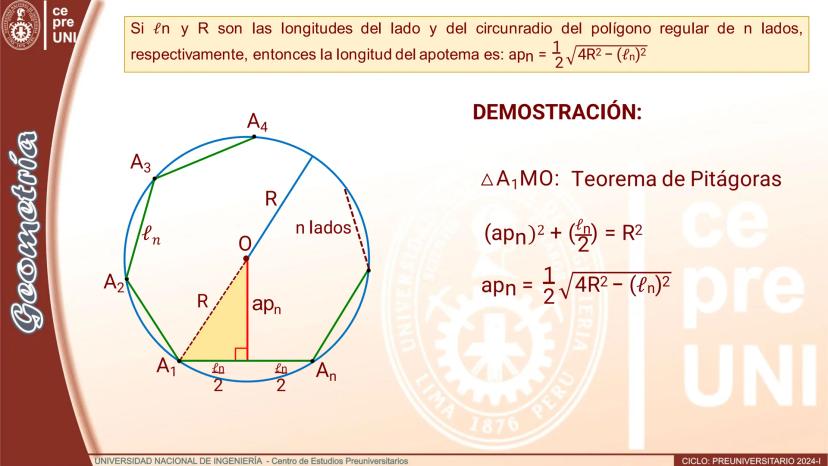
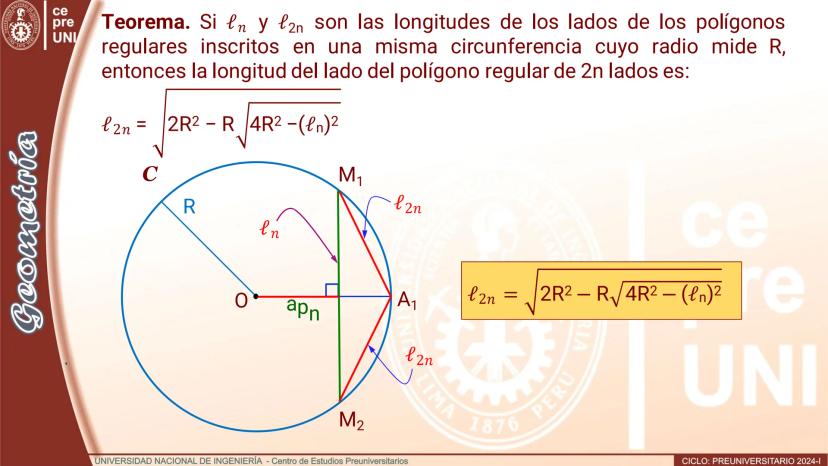
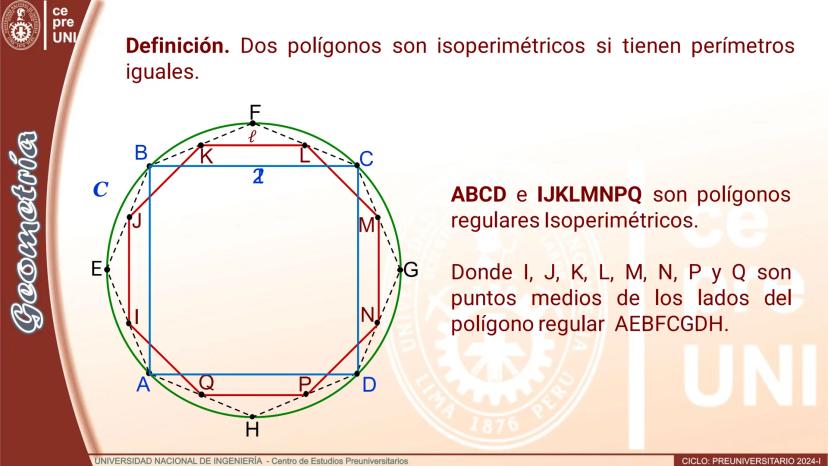
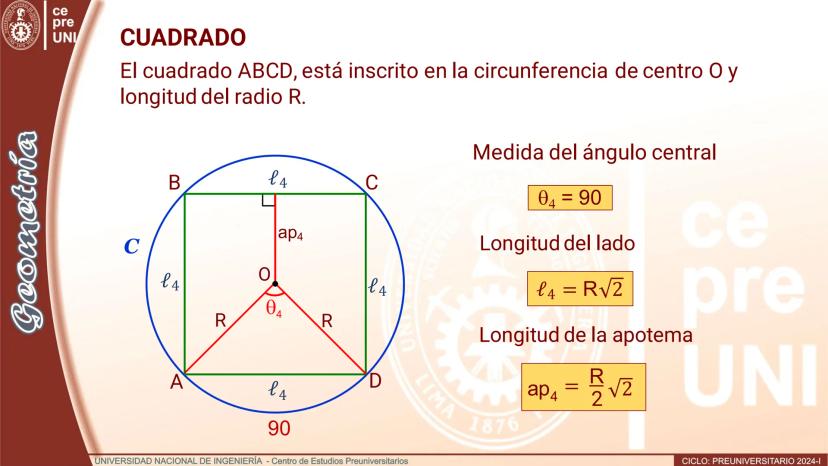
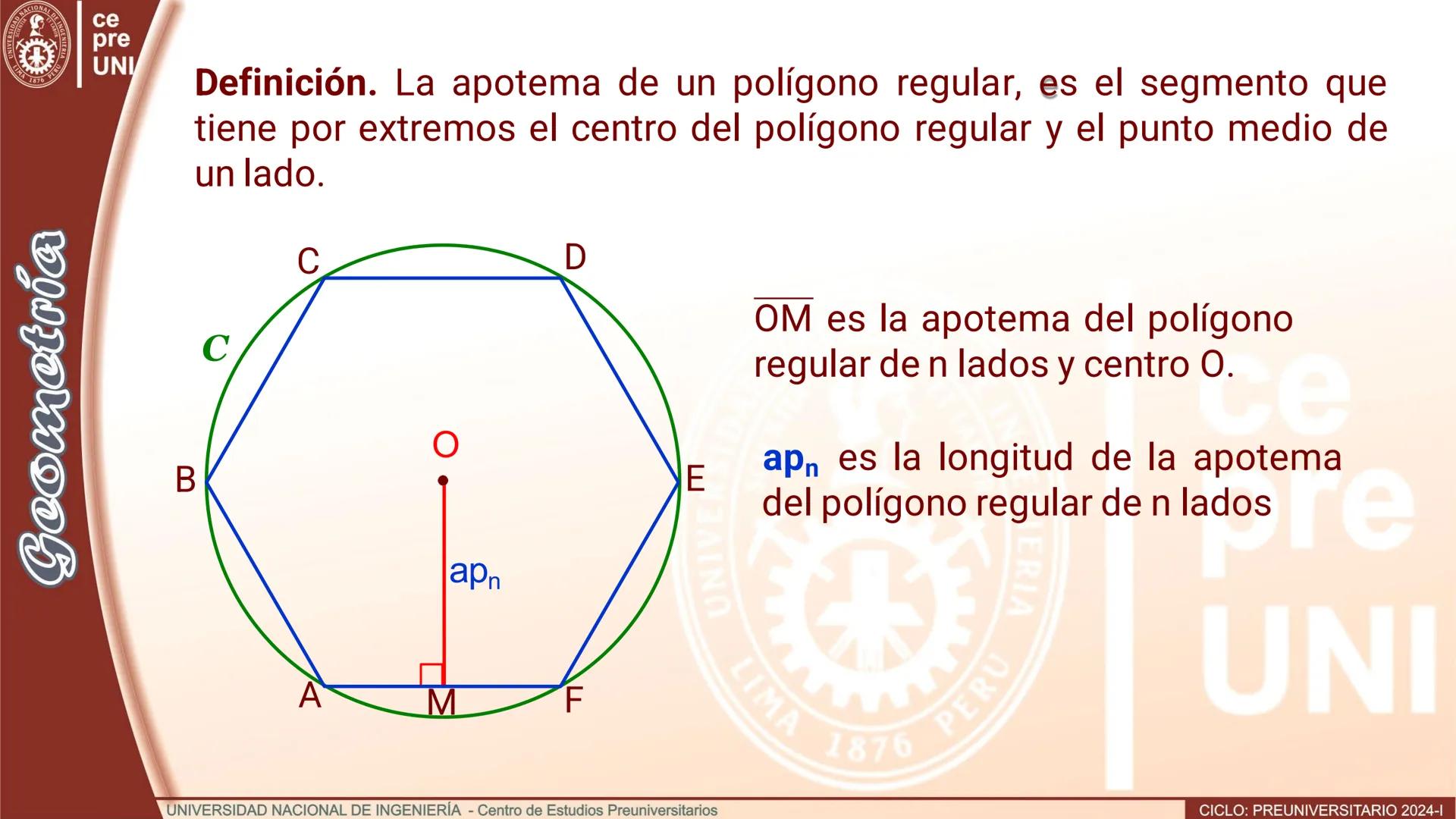
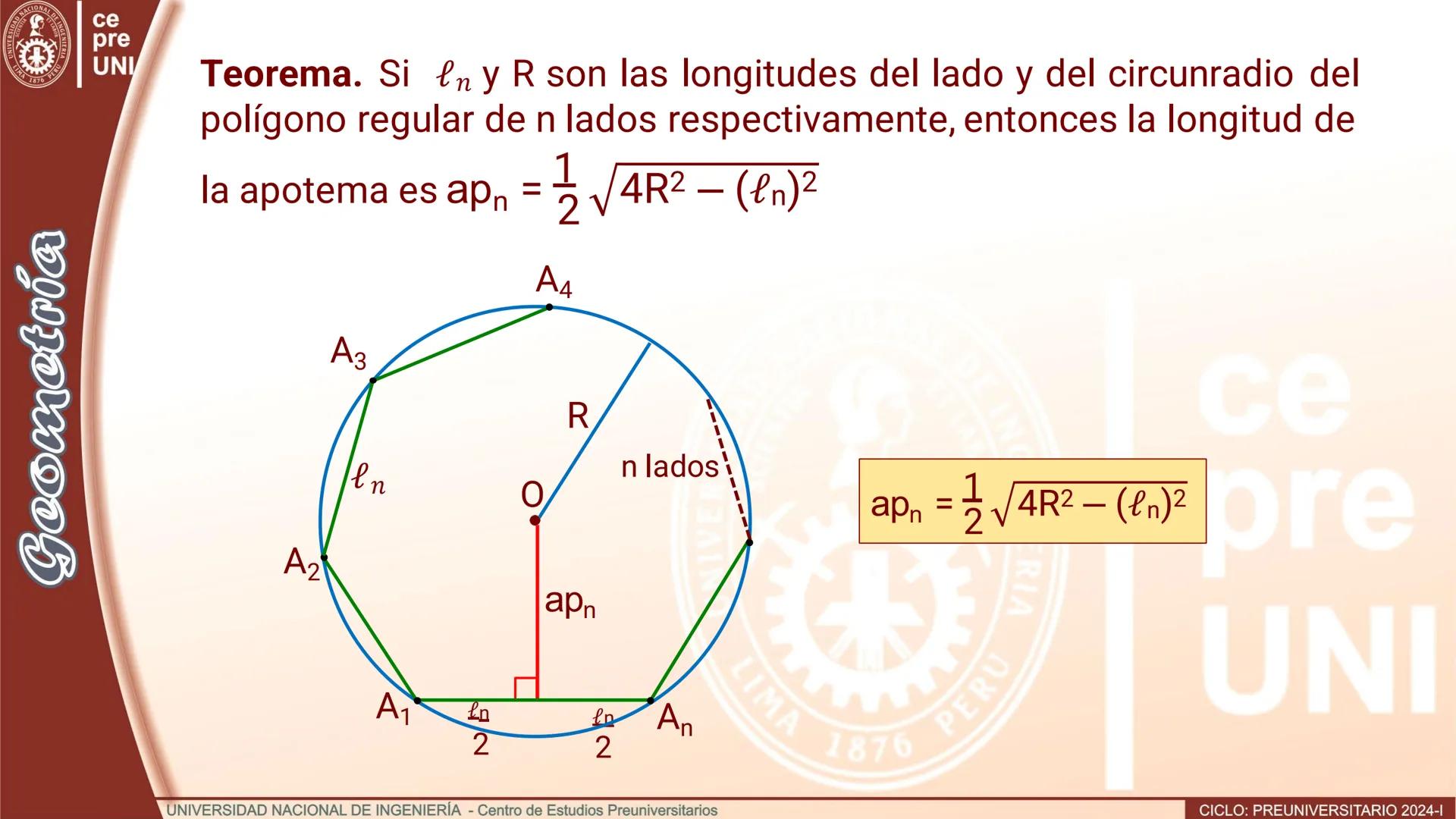
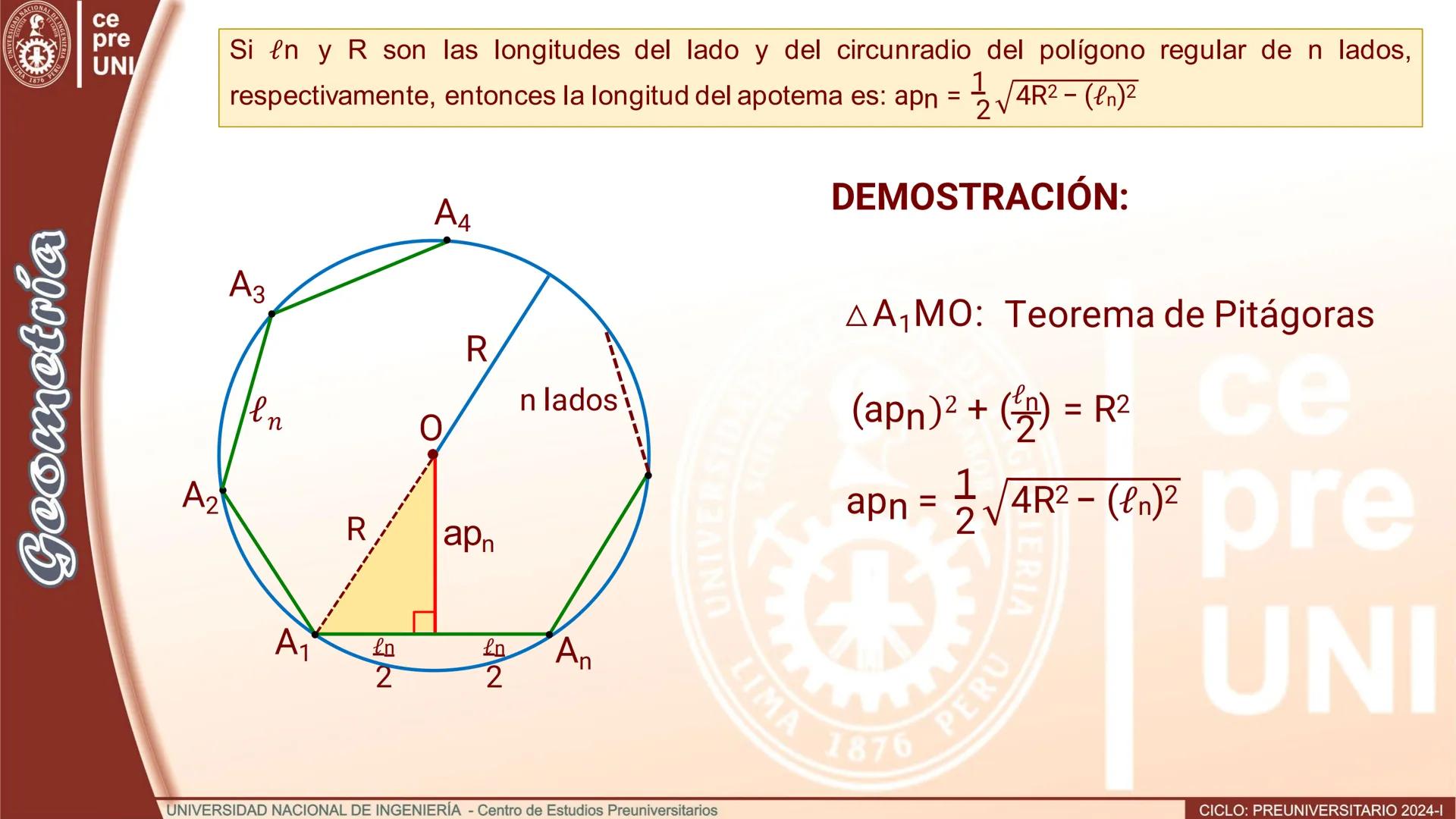
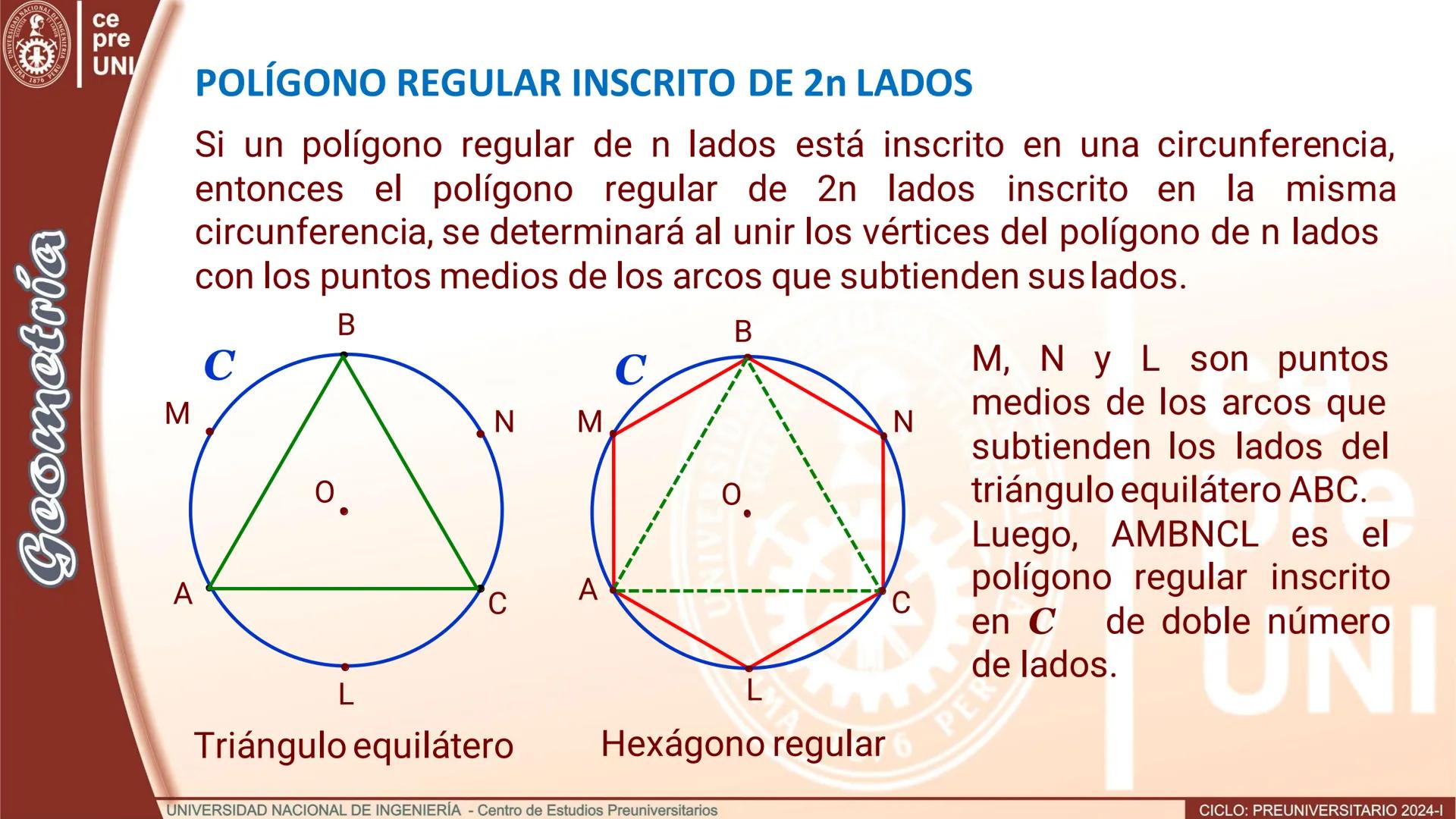
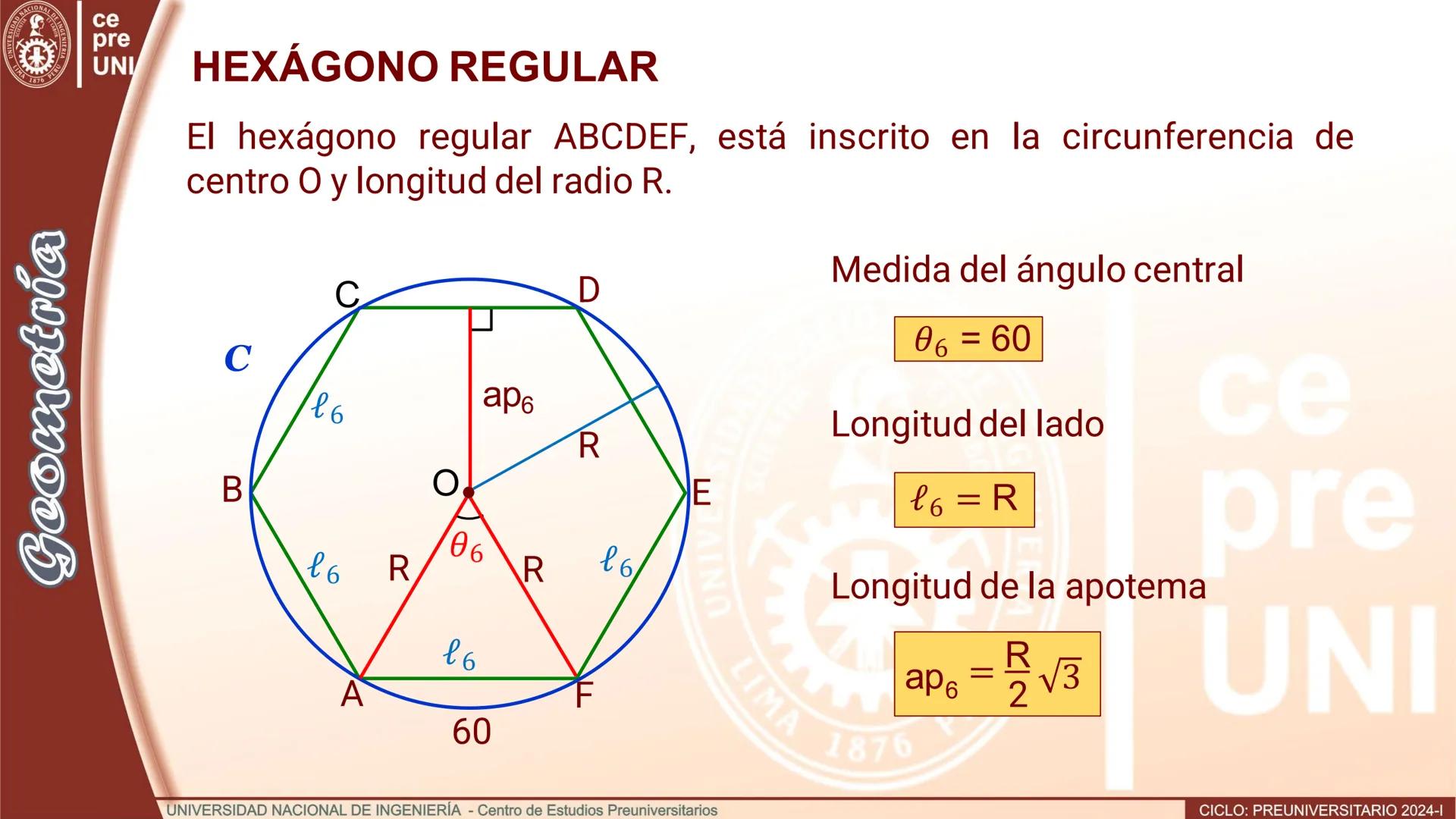
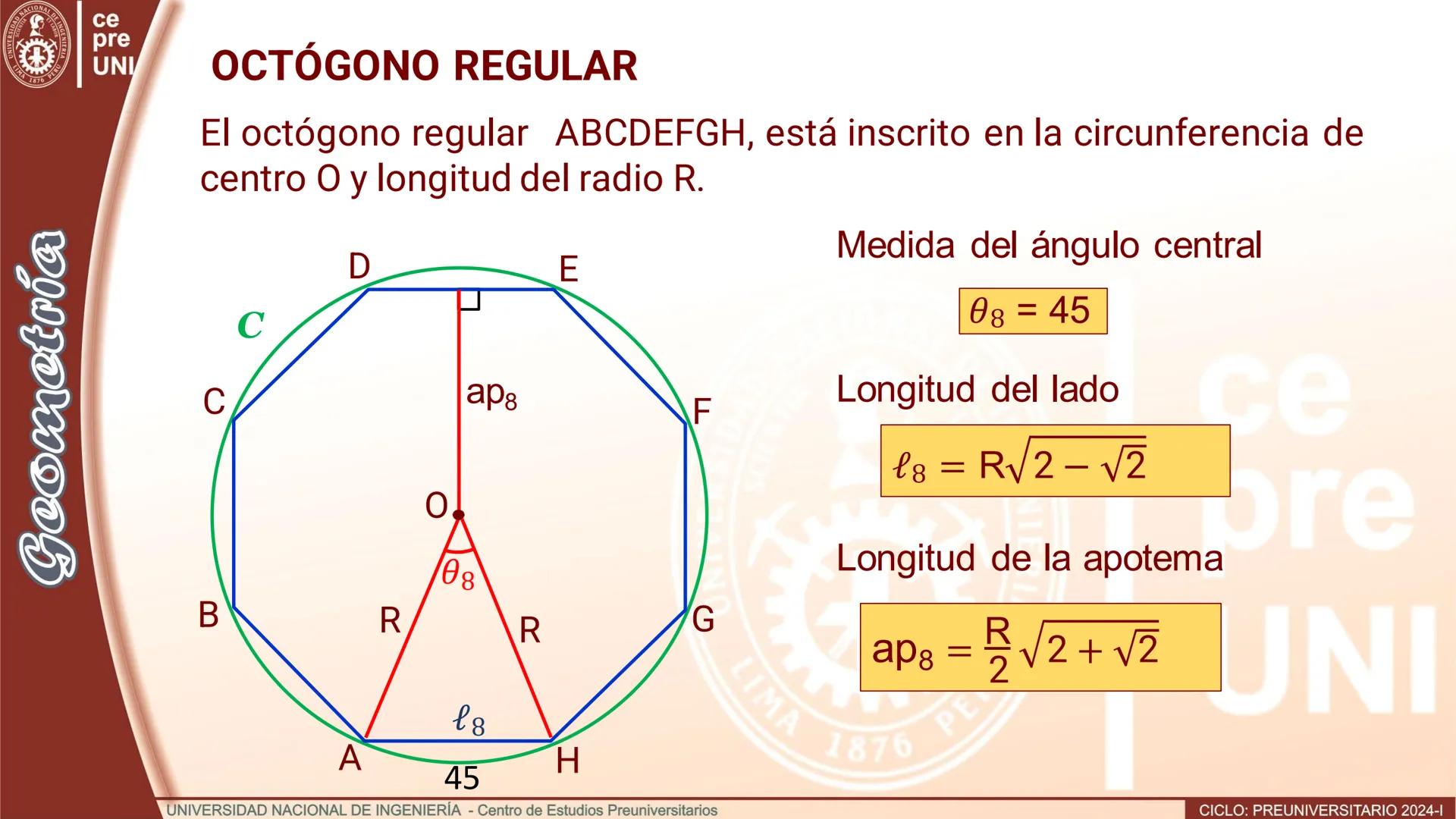
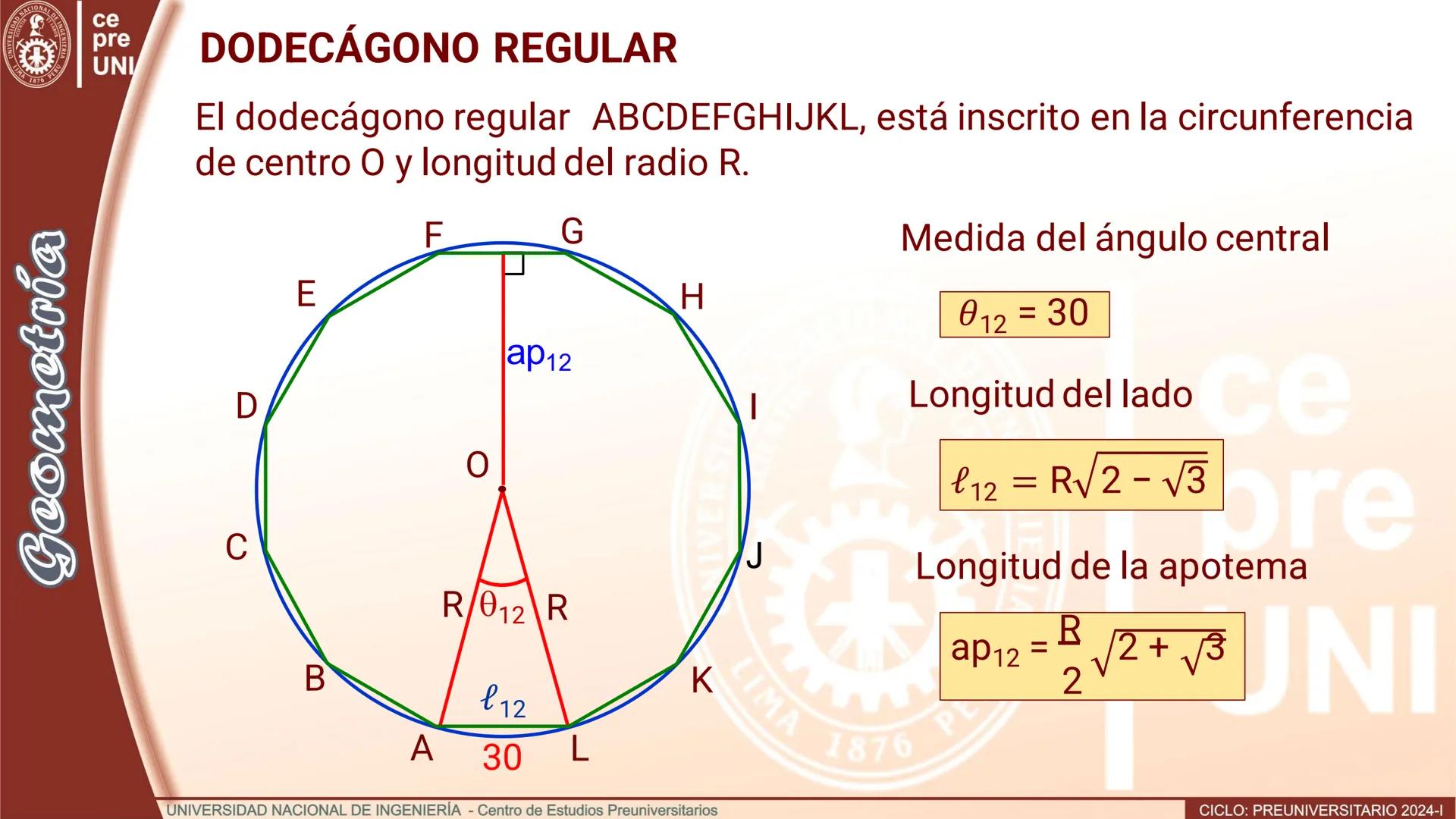
Polígono de doble número de lados
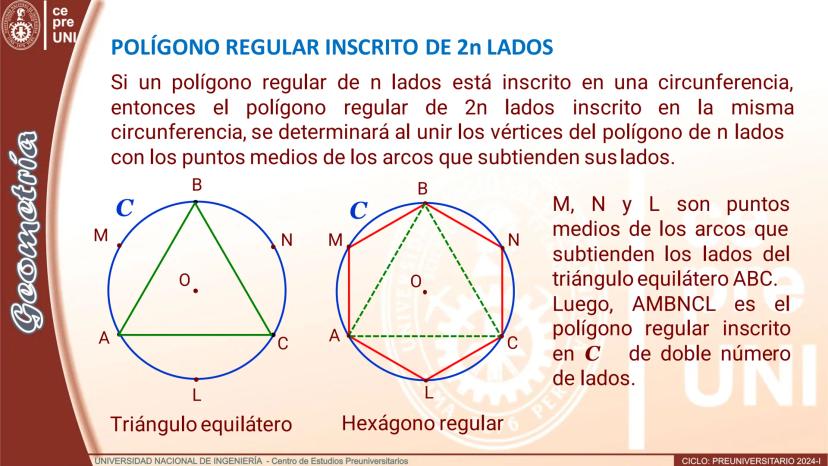
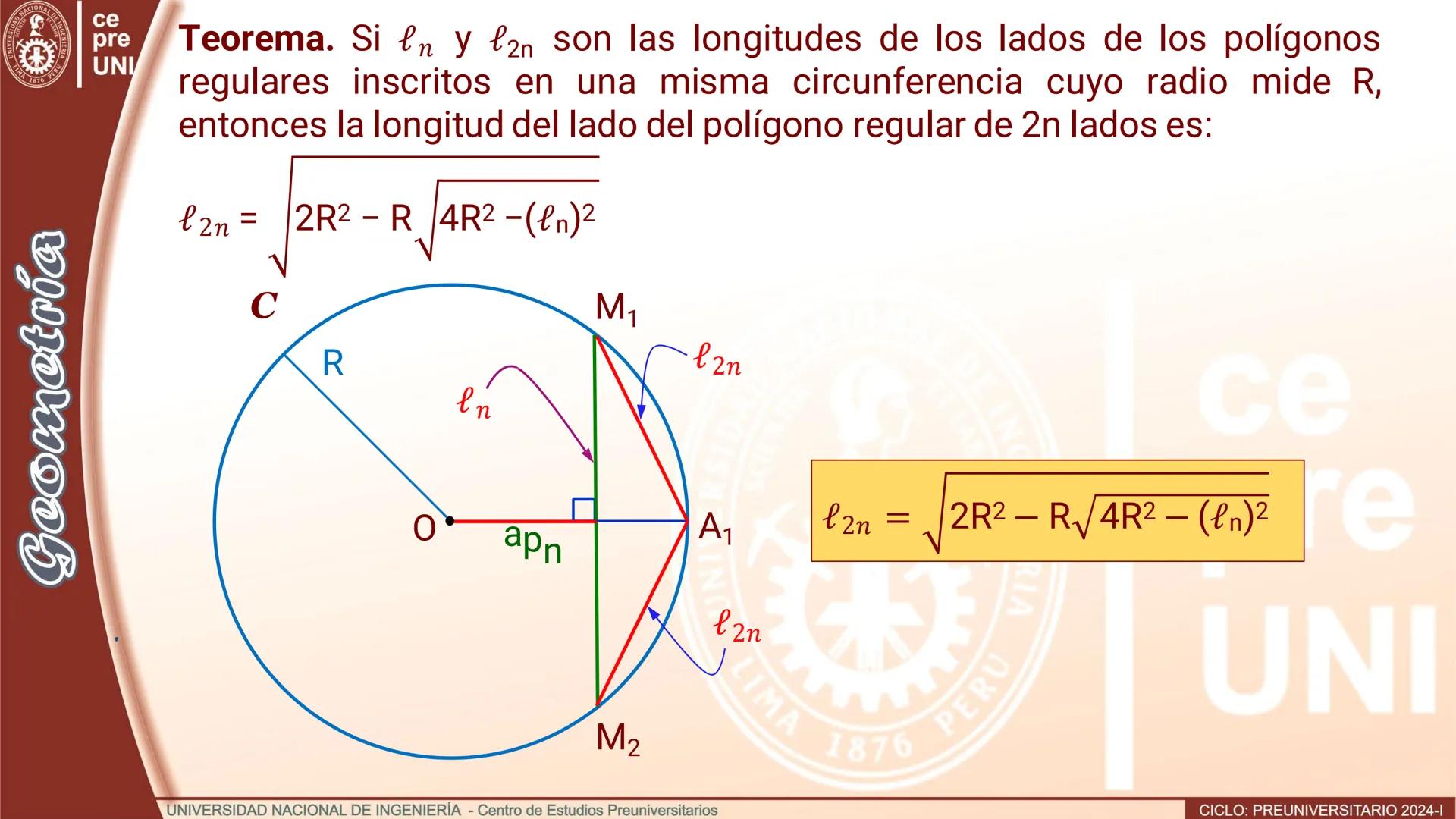
¿Cómo crear un polígono regular con el doble de lados? Es más fácil de lo que piensas. Si tienes un polígono regular de n lados inscrito en una circunferencia, puedes obtener uno de 2n lados agregando puntos estratégicos.
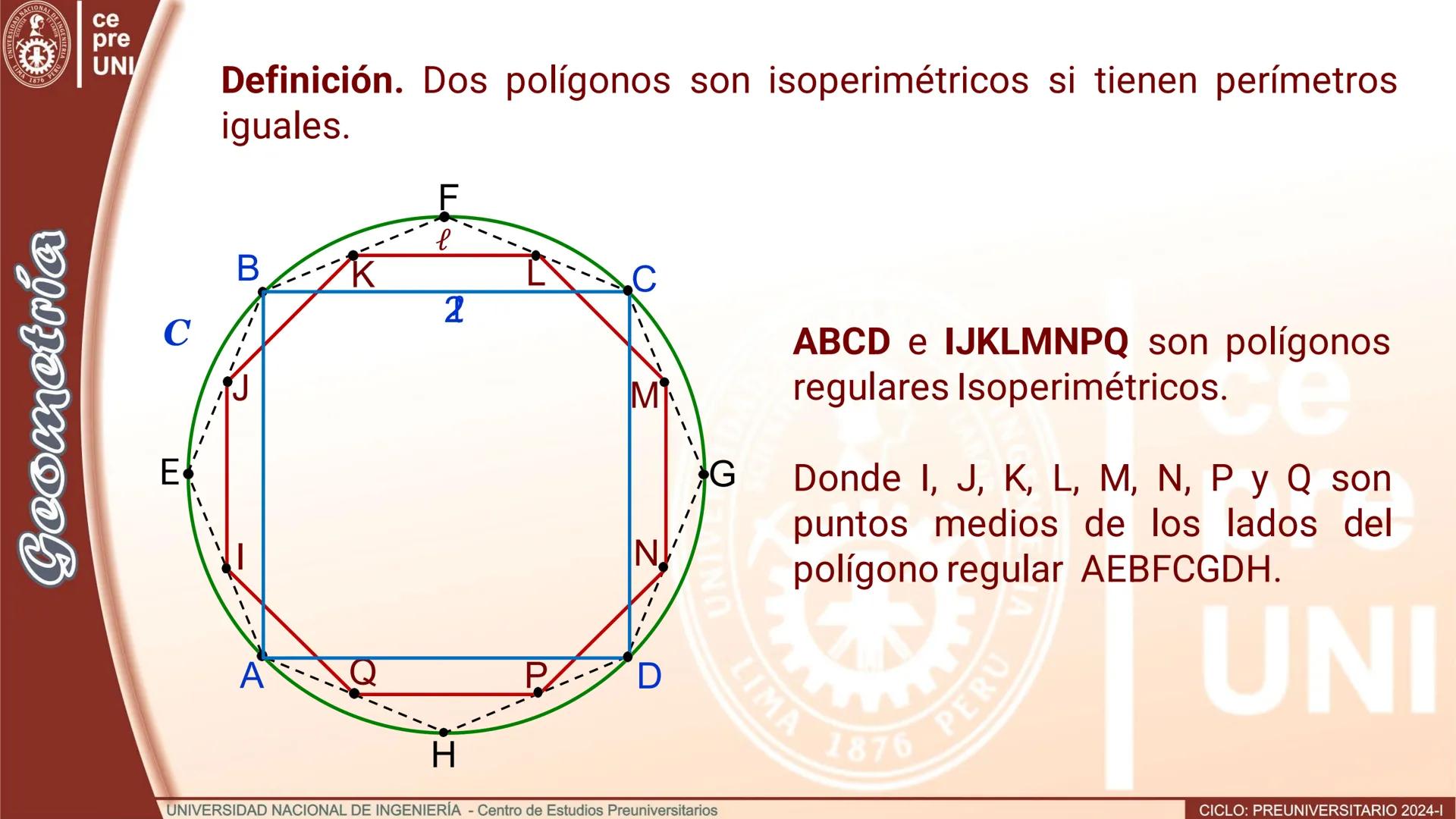
El truco es encontrar los puntos medios de los arcos que subtienden cada lado del polígono original. Estos puntos, junto con los vértices originales, forman un nuevo polígono regular con exactamente el doble de lados.
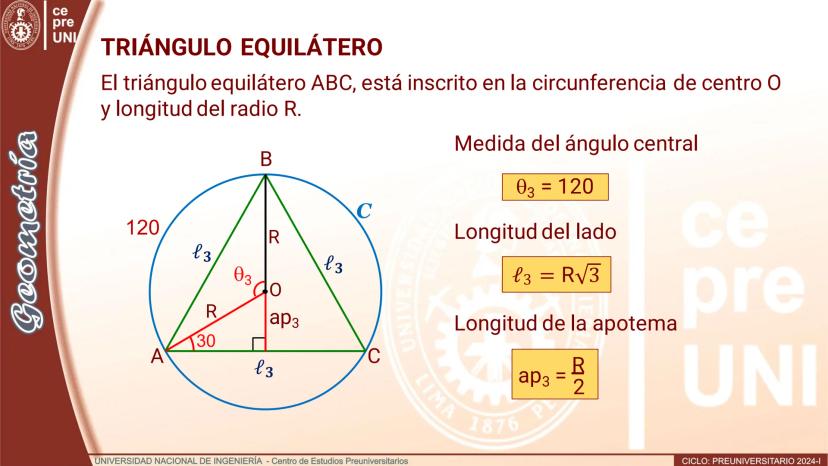
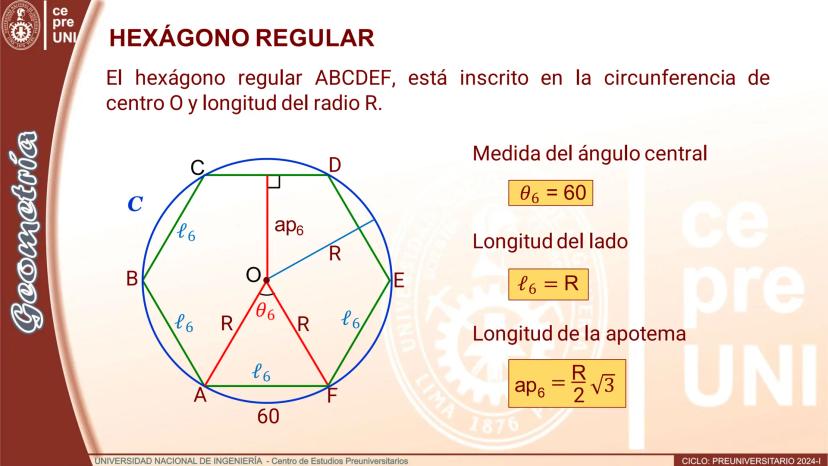
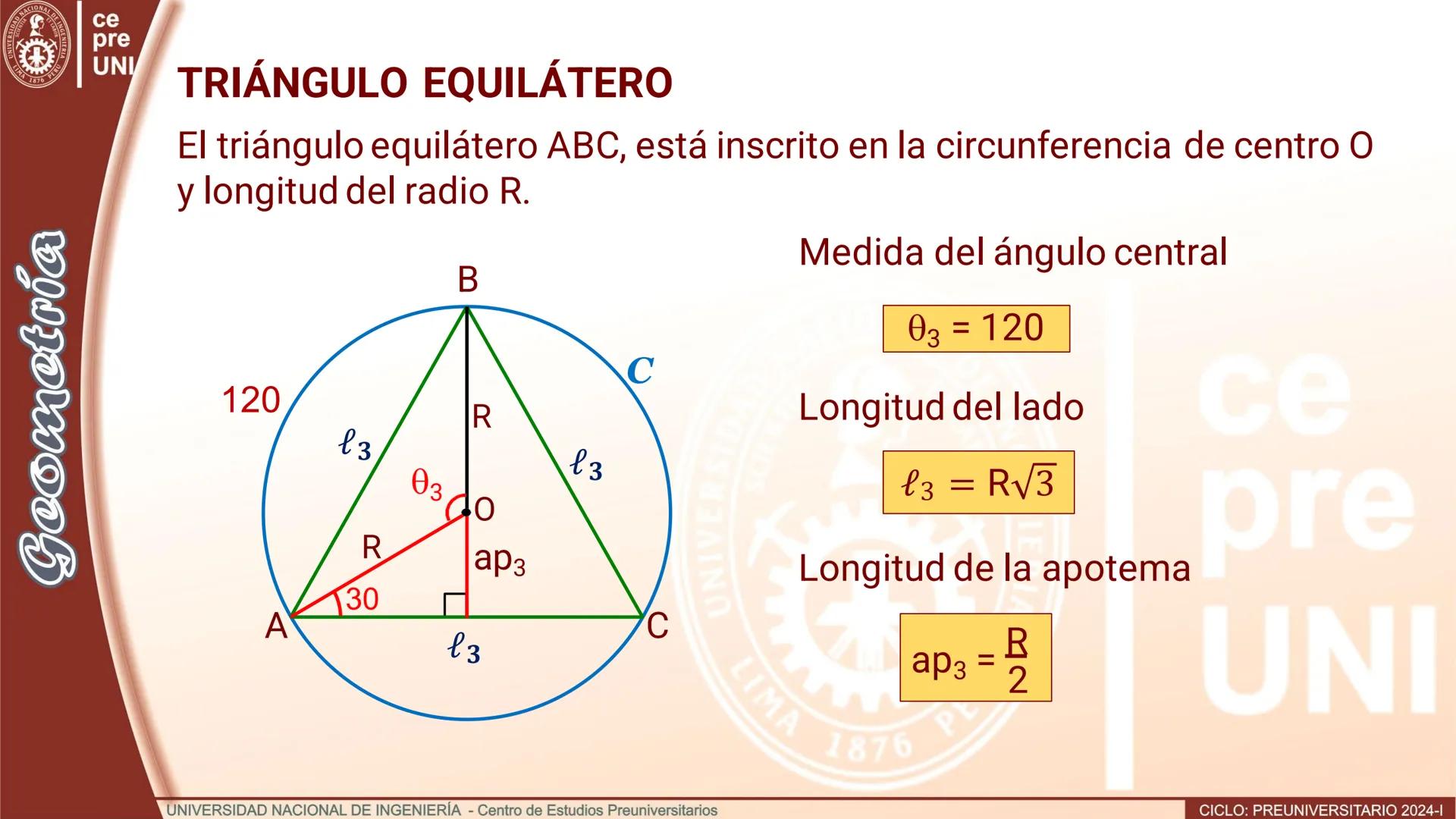
Por ejemplo, si tienes un triángulo equilátero (3 lados) inscrito en una circunferencia, al agregar los puntos medios de los arcos obtienes un hexágono regular (6 lados). El proceso conserva la regularidad del polígono.
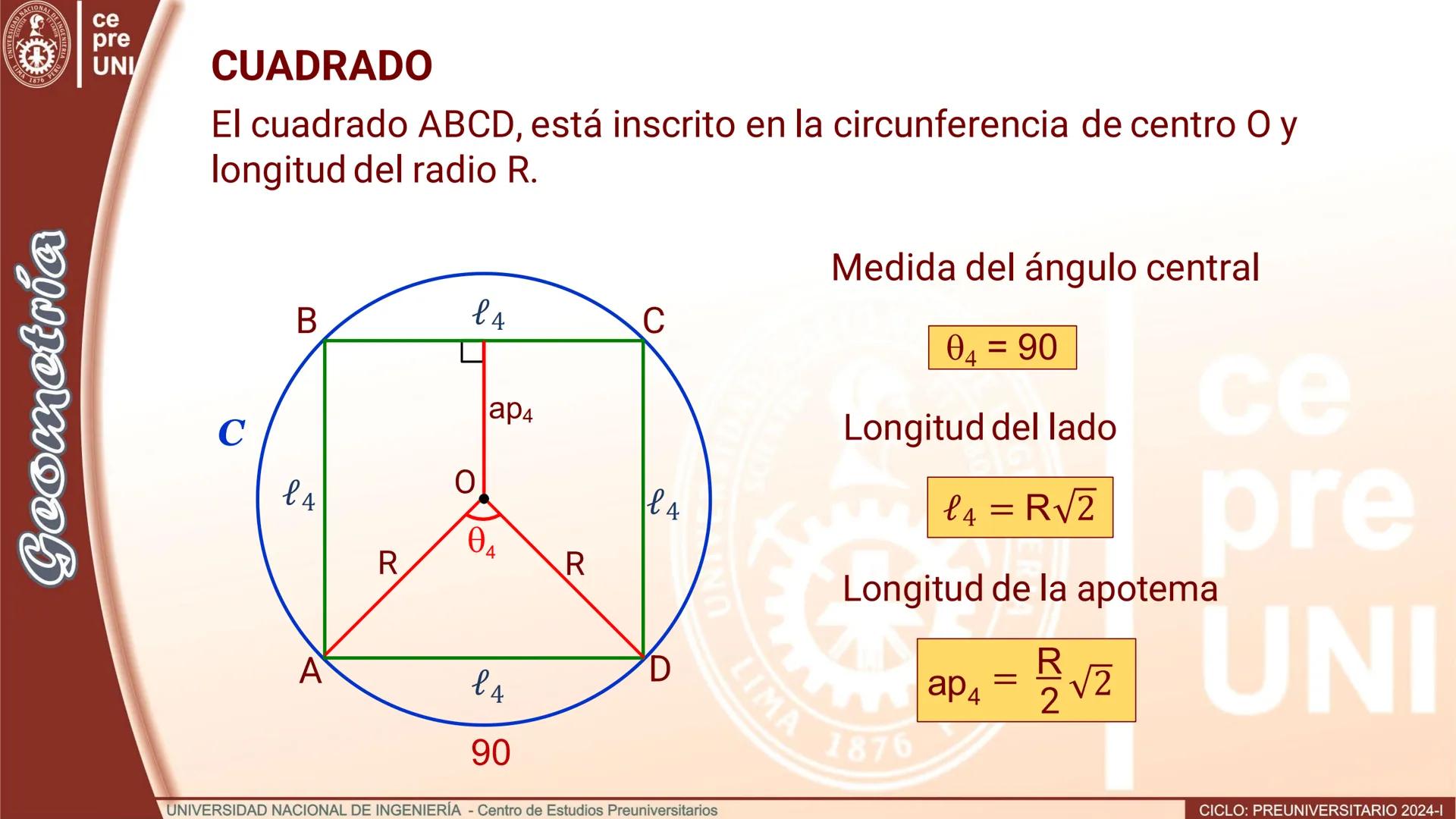
¡Dato interesante! Este método te permite crear polígonos regulares de 6, 12, 24, 48... lados, empezando desde un simple triángulo equilátero.