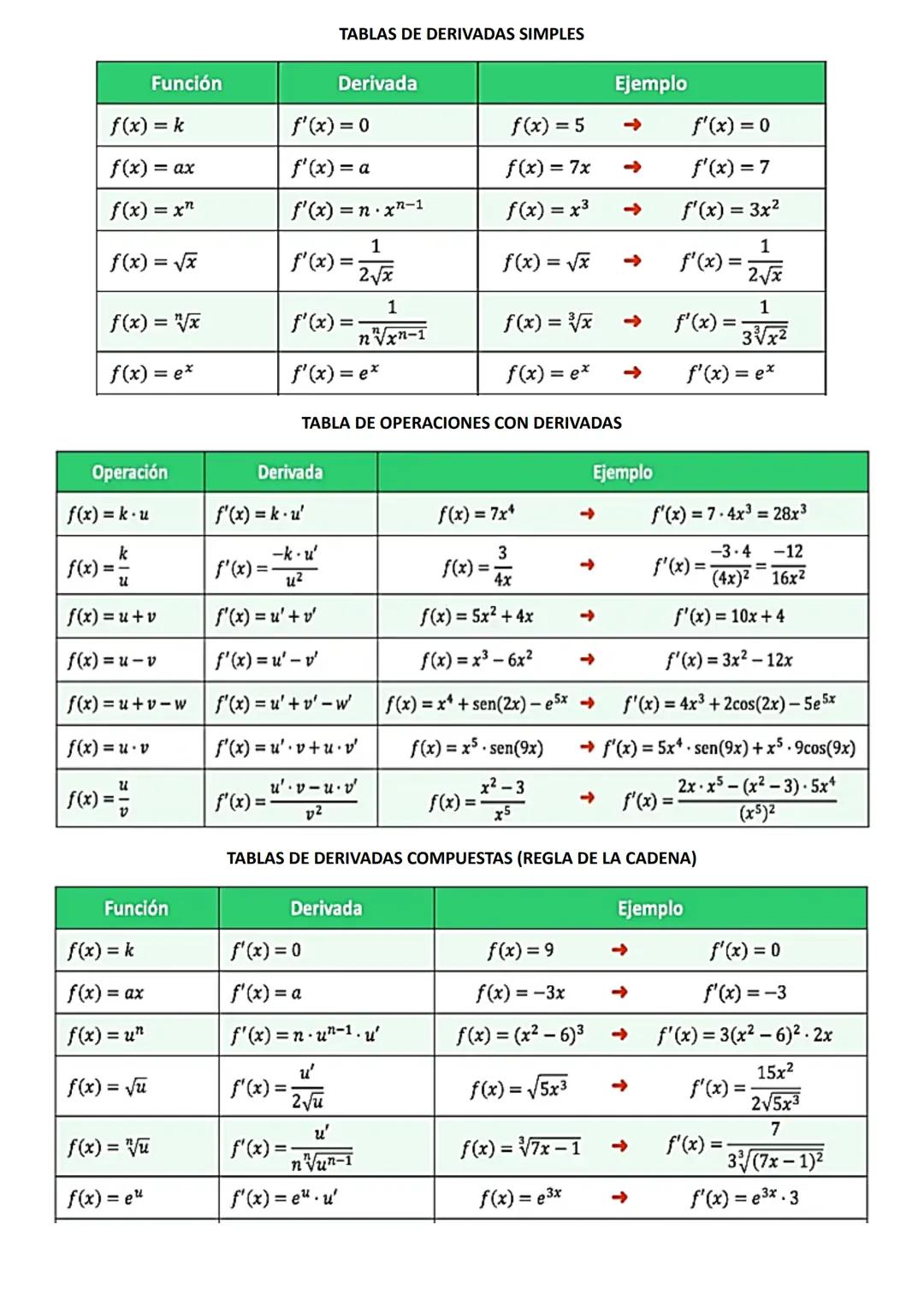
Interpretación Geométrica: ¿Qué Significan Realmente las Derivadas?
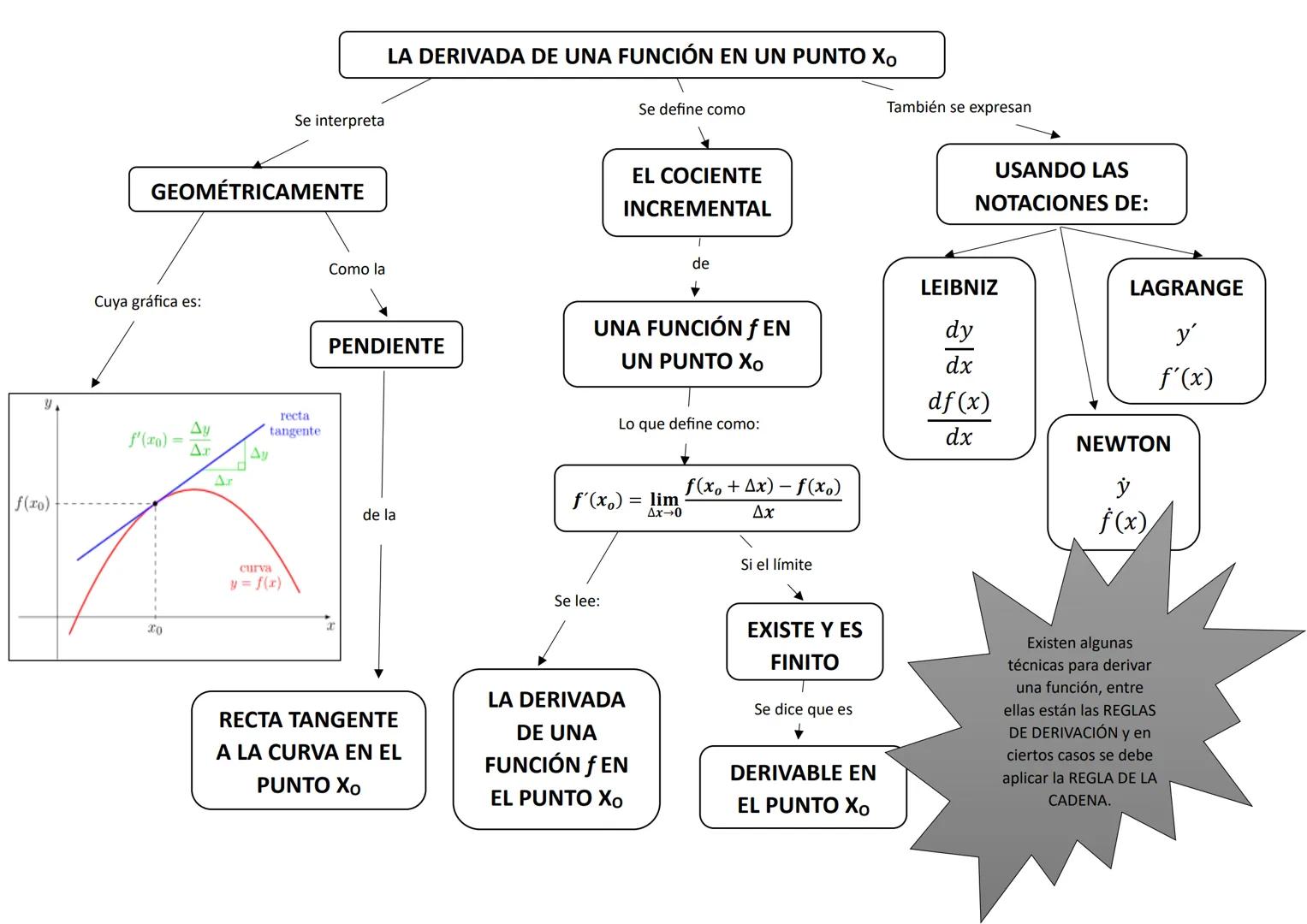
La derivada no es solo una fórmula matemática abstracta: tiene un significado visual súper claro que te ayudará a entender mejor los problemas. La derivada en un punto es la pendiente de la recta tangente a la curva en ese punto específico.
Imagínate dibujando una línea recta que apenas toca una curva en un solo punto, sin cortarla. Esa es la recta tangente, y su inclinación (pendiente) es exactamente el valor de la derivada en ese punto. Si la derivada es positiva, la función está creciendo; si es negativa, está decreciendo.
Matemáticamente, esto se define como el límite del cociente incremental: f′(x0)=limΔx→0Δxf(x0+Δx)−f(x0). Básicamente, estás midiendo qué tan rápido cambia la función cuando te mueves una distancia infinitamente pequeña.
Existen diferentes notaciones para expresar derivadas. Puedes escribir f′(x) (notación de Lagrange), dxdy (notación de Leibniz), o y˙ (notación de Newton). Todas significan lo mismo, solo cambia el contexto donde se usan.
Consejo visual: Siempre piensa en la derivada como la "velocidad" con la que sube o baja una función. Te ayudará a interpretar resultados de manera intuitiva.