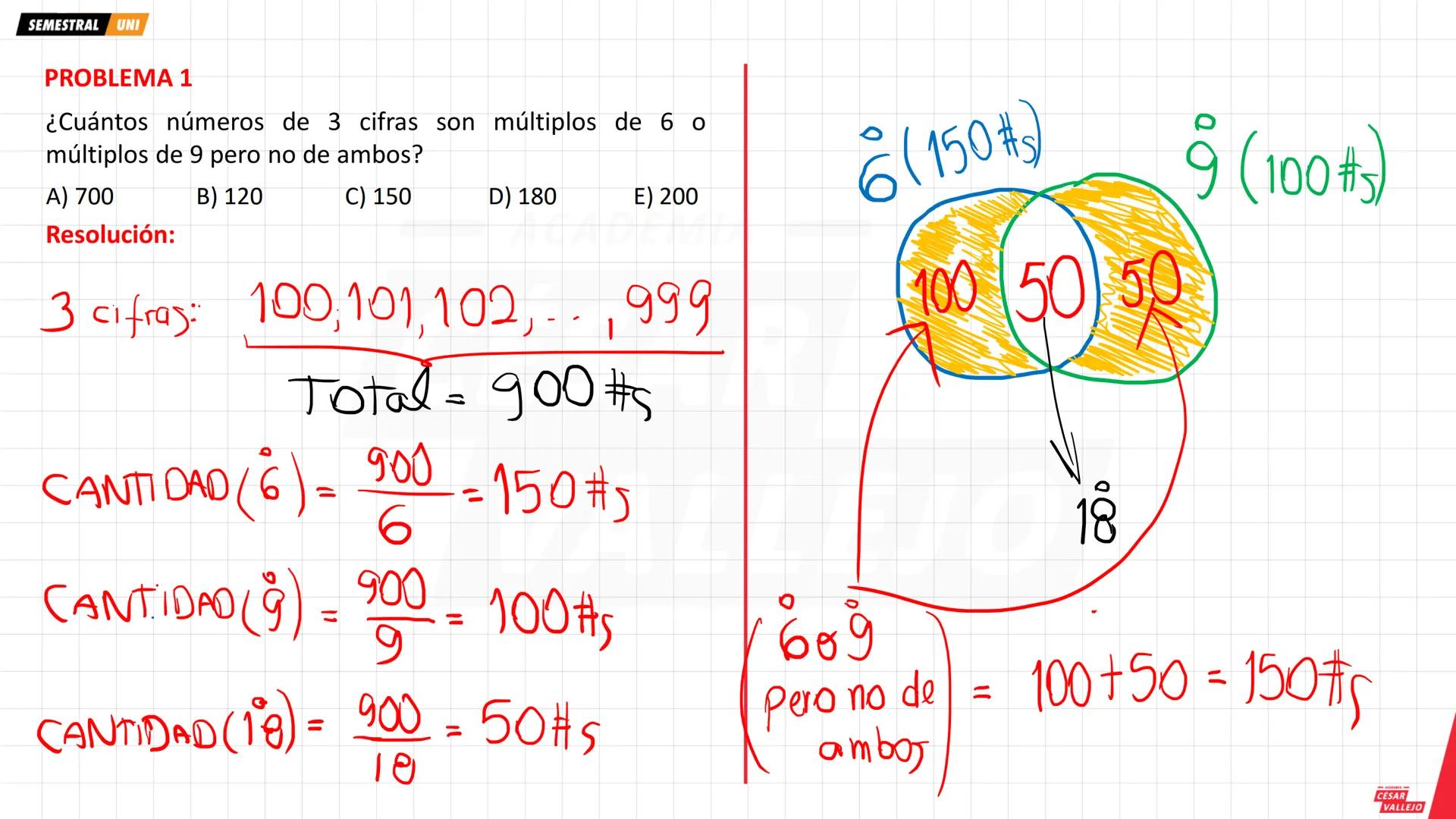
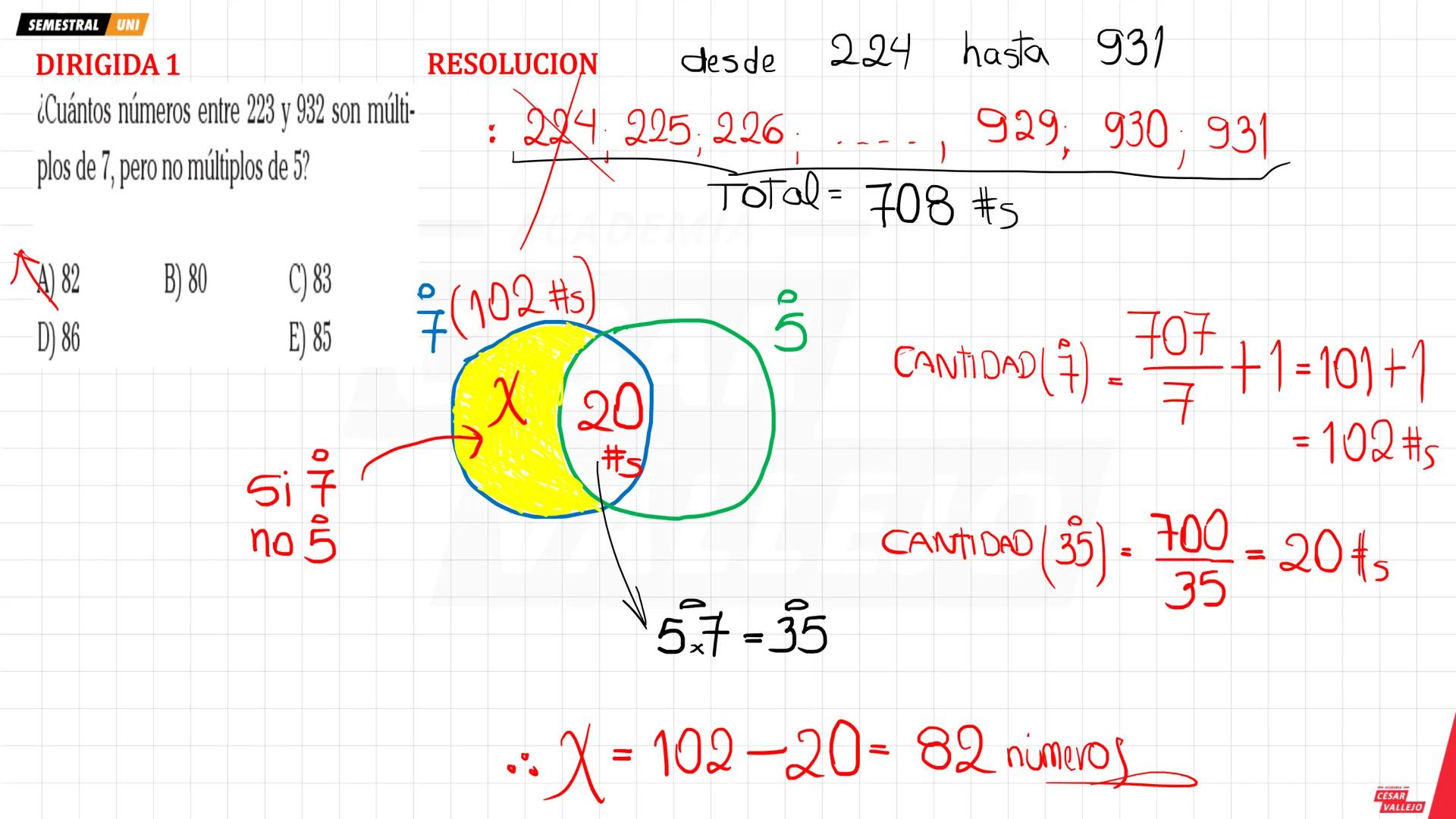
Conteo de múltiplos en rangos específicos
Contar múltiplos dentro de un rango es una habilidad súper útil que aparece frecuentemente en exámenes. Para números de 2 cifras que son múltiplos de 6, simplemente aplicamos la fórmula práctica.
Los números de 2 cifras van del 10 al 99, lo que nos da un total de 90 números. Para encontrar cuántos son múltiplos de 6, dividimos: 90 ÷ 6 = 15 números.
Los múltiplos de 6 entre 10 y 99 son: 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96. Como ves, efectivamente son 15 números.
Tip de estudio: Para cualquier rango de números, la cantidad de múltiplos se calcula dividiendo la cantidad total de números entre el módulo.