Números Simples: La Base de Todo
¿Sabías que todos los números enteros positivos se pueden clasificar según sus divisores? Los números simples son aquellos que tienen como máximo dos divisores, y se dividen en dos categorías súper importantes.
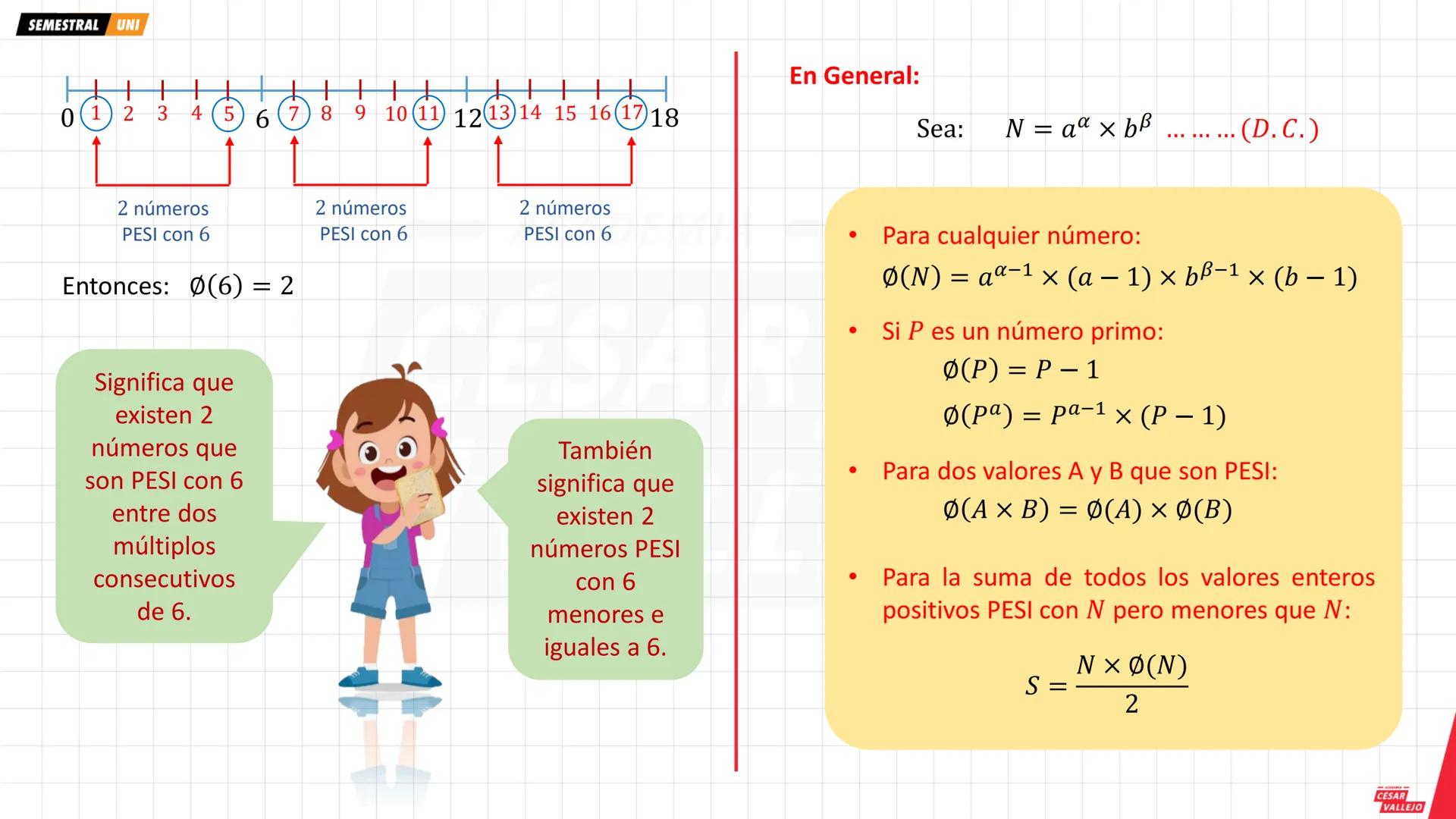
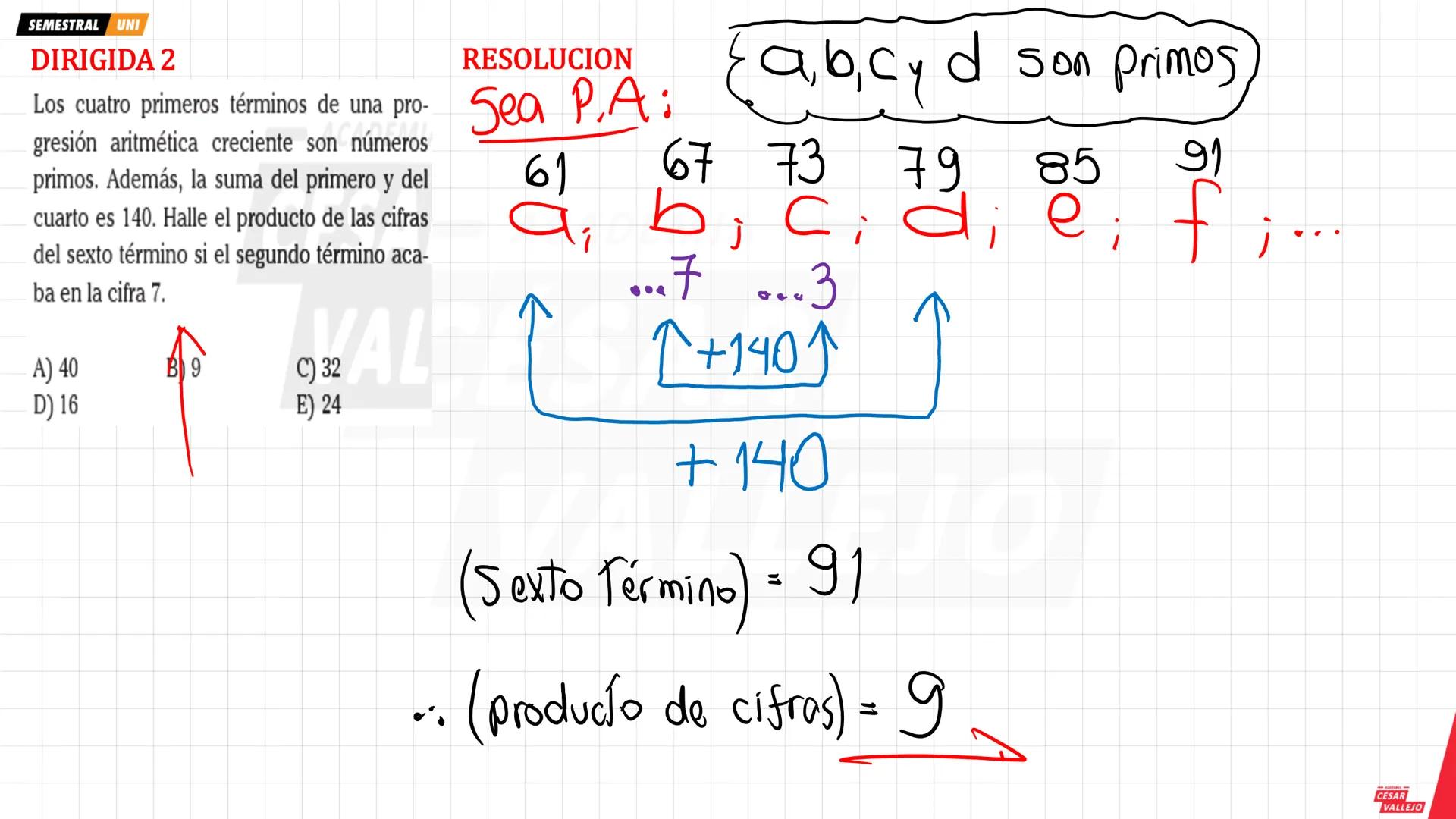
La unidad es única: el número 1 tiene solo un divisor (él mismo). Los números primos son los que tienen exactamente dos divisores: la unidad y el mismo número. Por ejemplo: 2, 3, 5, 7, 11, 13, 17, 19...
El 2 es el menor número primo y el único primo par. Todos los demás primos son impares, lo que te facilita identificarlos en los ejercicios.
💡 Dato clave: Memoriza los primeros primos: 2, 3, 5, 7, 11, 13, 17, 19, 23. Te servirán en muchos problemas.