Sistemas de Numeración y Sus Bases
Cada sistema tiene reglas específicas que debes conocer para los exámenes. El sistema decimal que usas diariamente es solo uno de muchos.
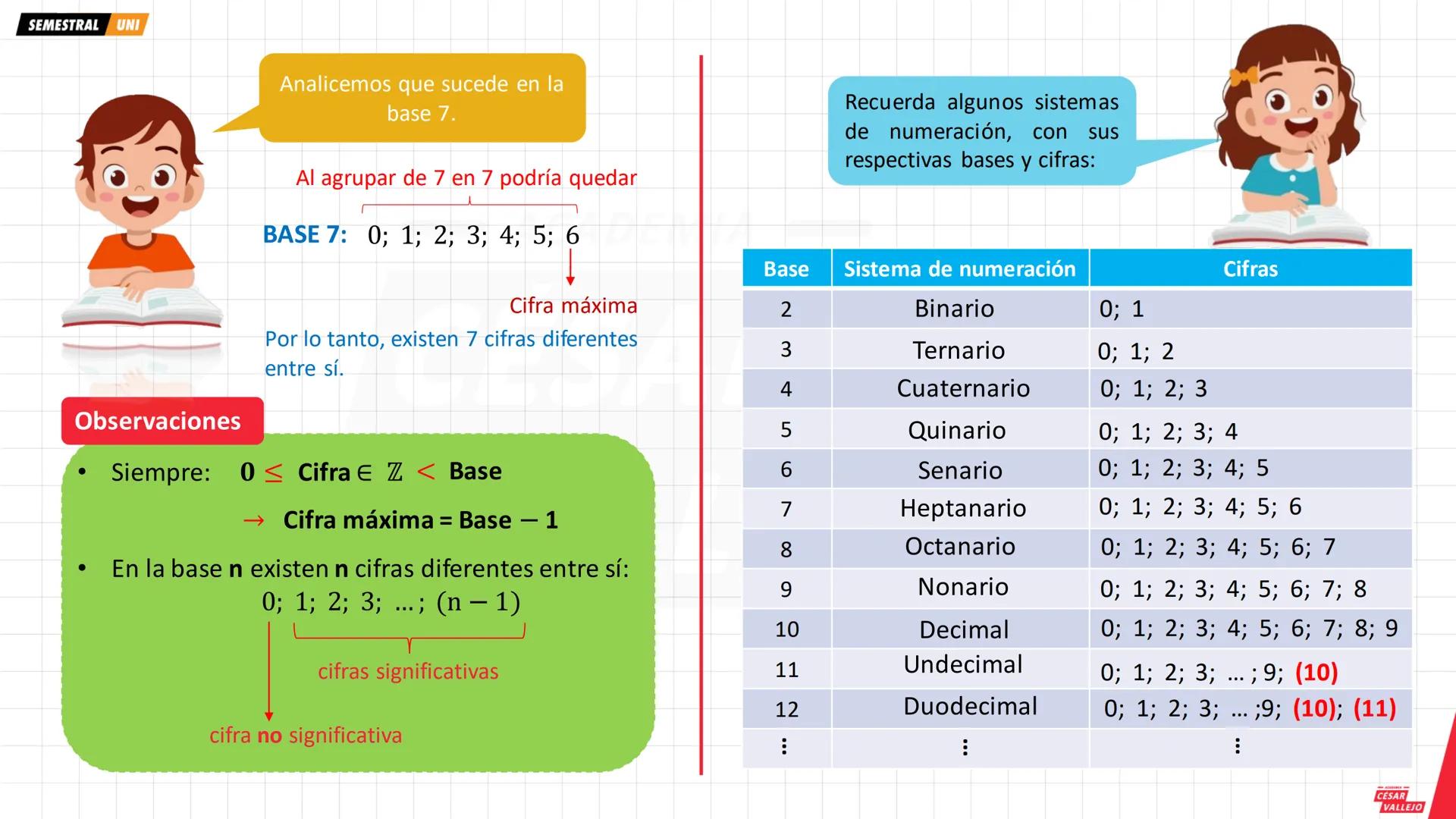
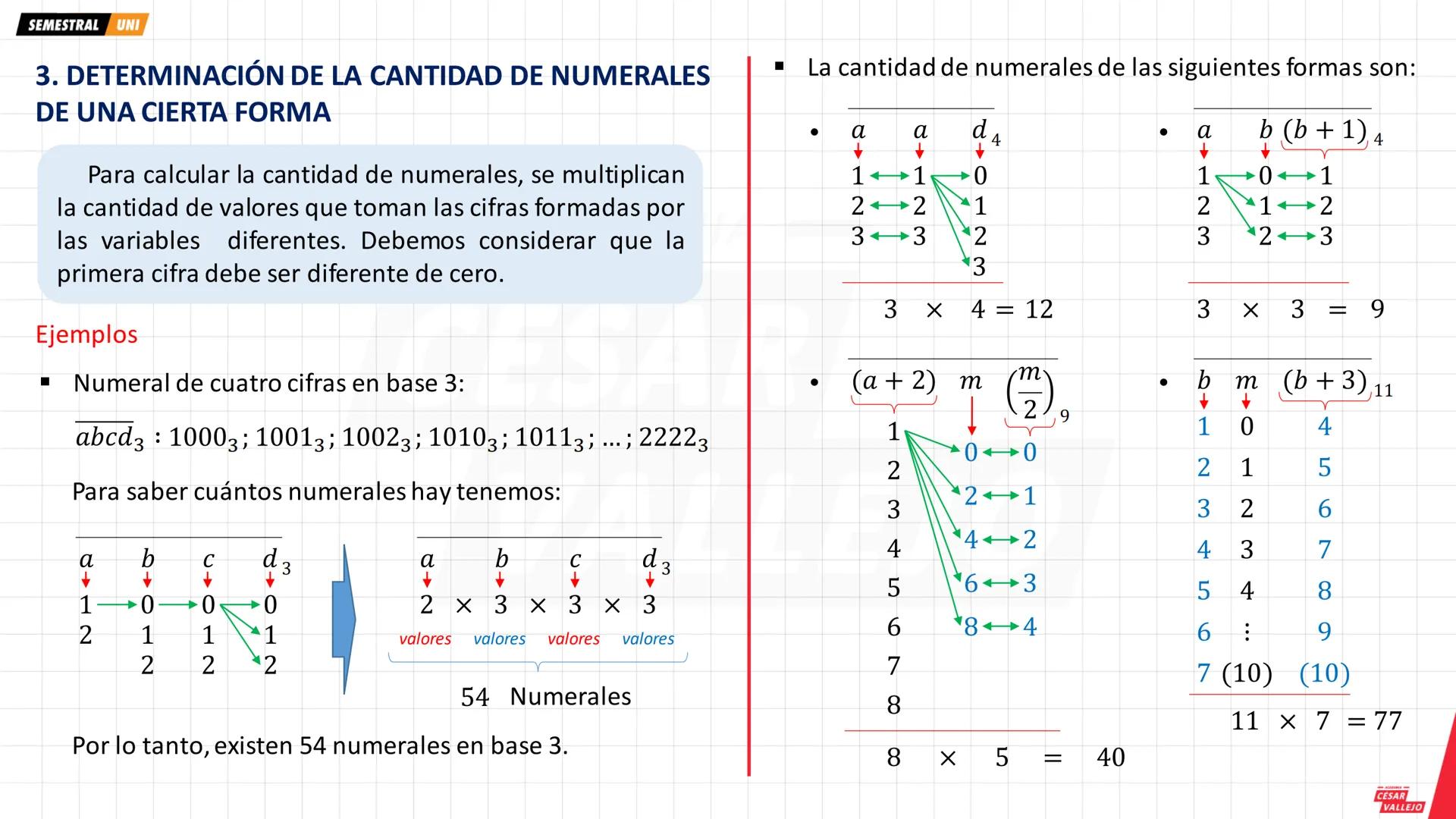
Los sistemas más comunes van desde binario (base 2) hasta duodecimal (base 12). En base n, solo puedes usar n cifras diferentes: desde 0 hasta n−1. Por ejemplo, en base 7 solo usas: 0, 1, 2, 3, 4, 5, 6.
La regla de oro es: 0 ≤ Cifra < Base. Esto significa que la cifra máxima siempre es Base−1. En base 8, la cifra máxima es 7; en base 5, es 4.
Recuerda: Cuando veas paréntesis como (10) en base 12, representa una sola cifra, no dos números separados.