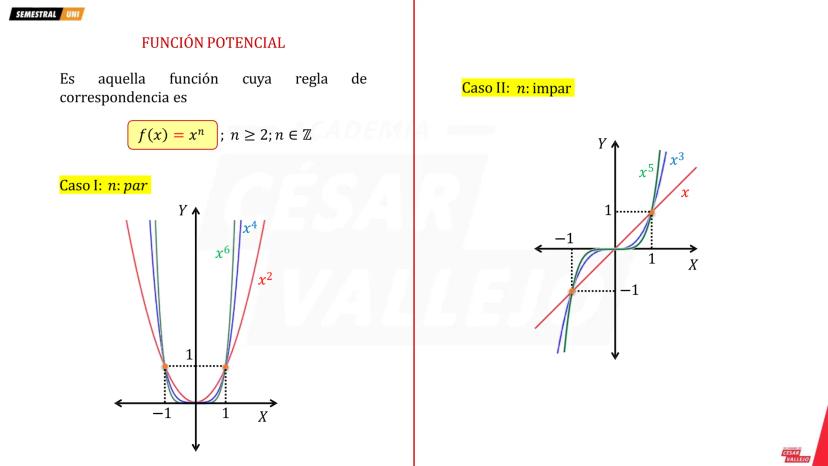
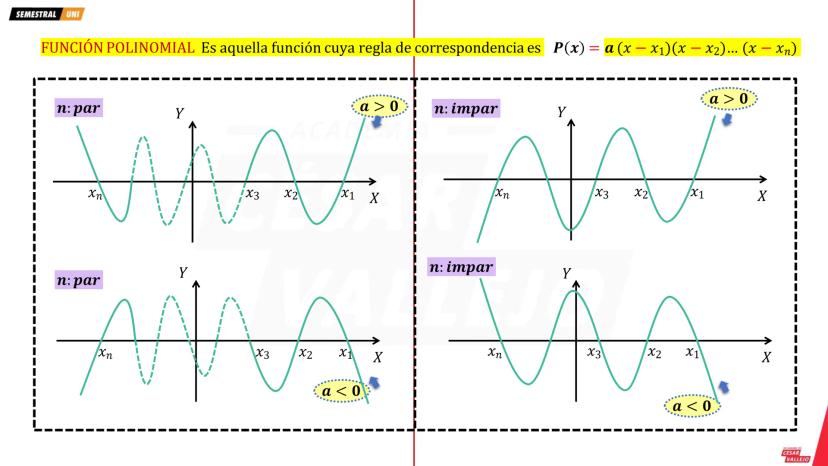
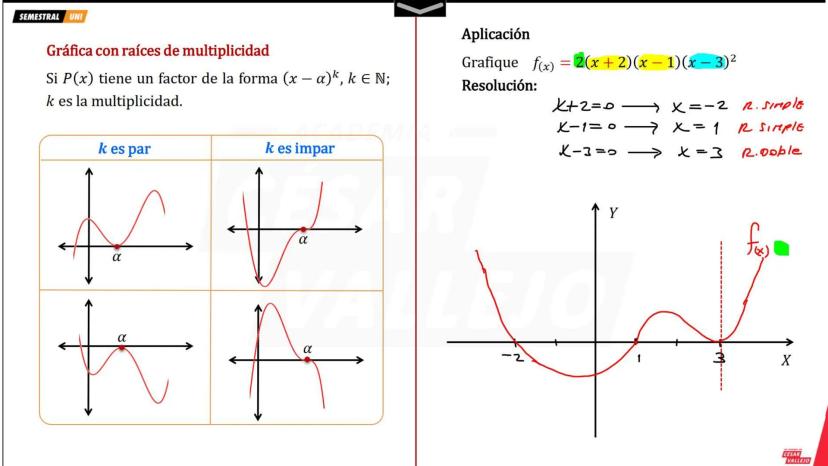
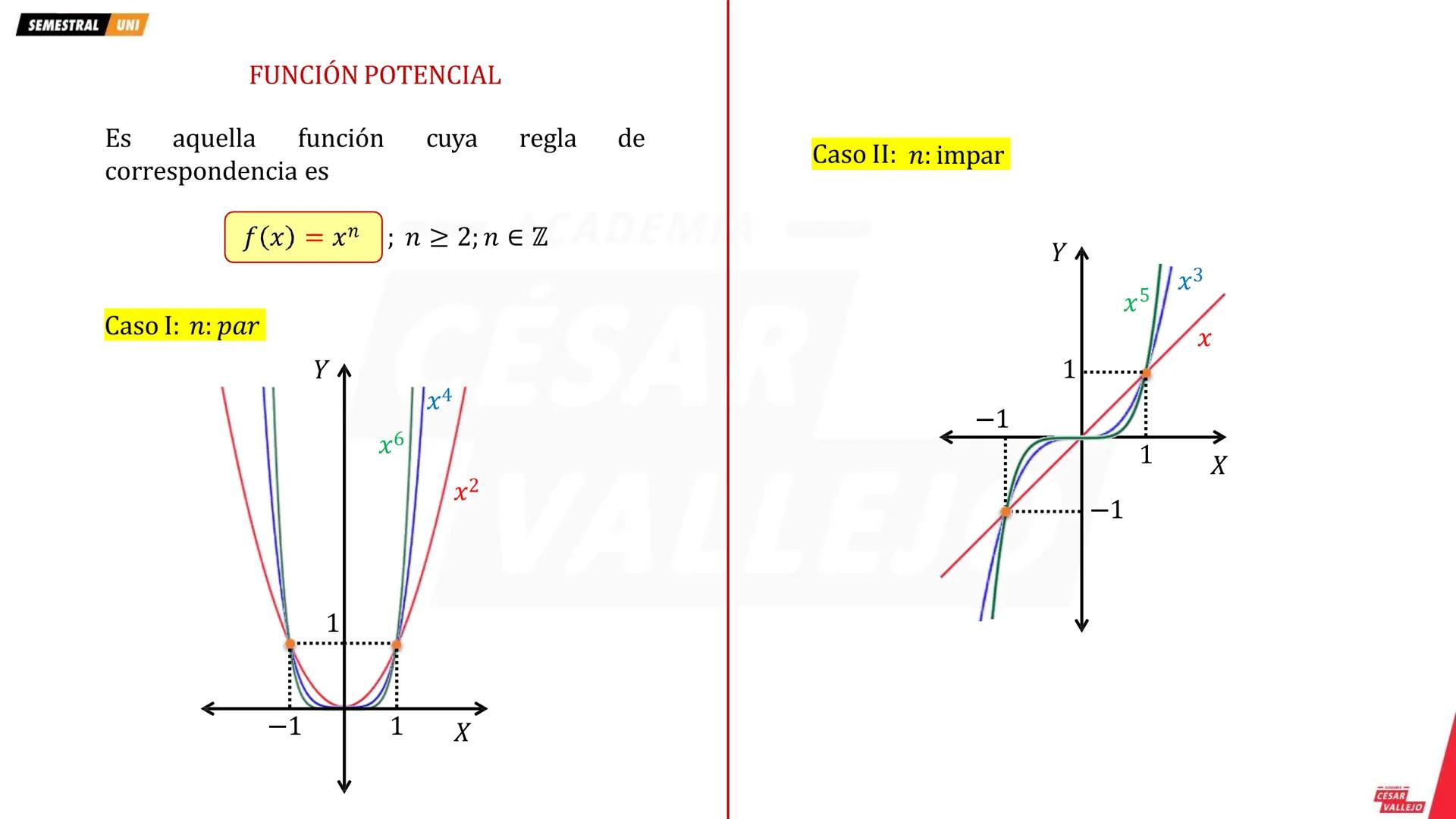
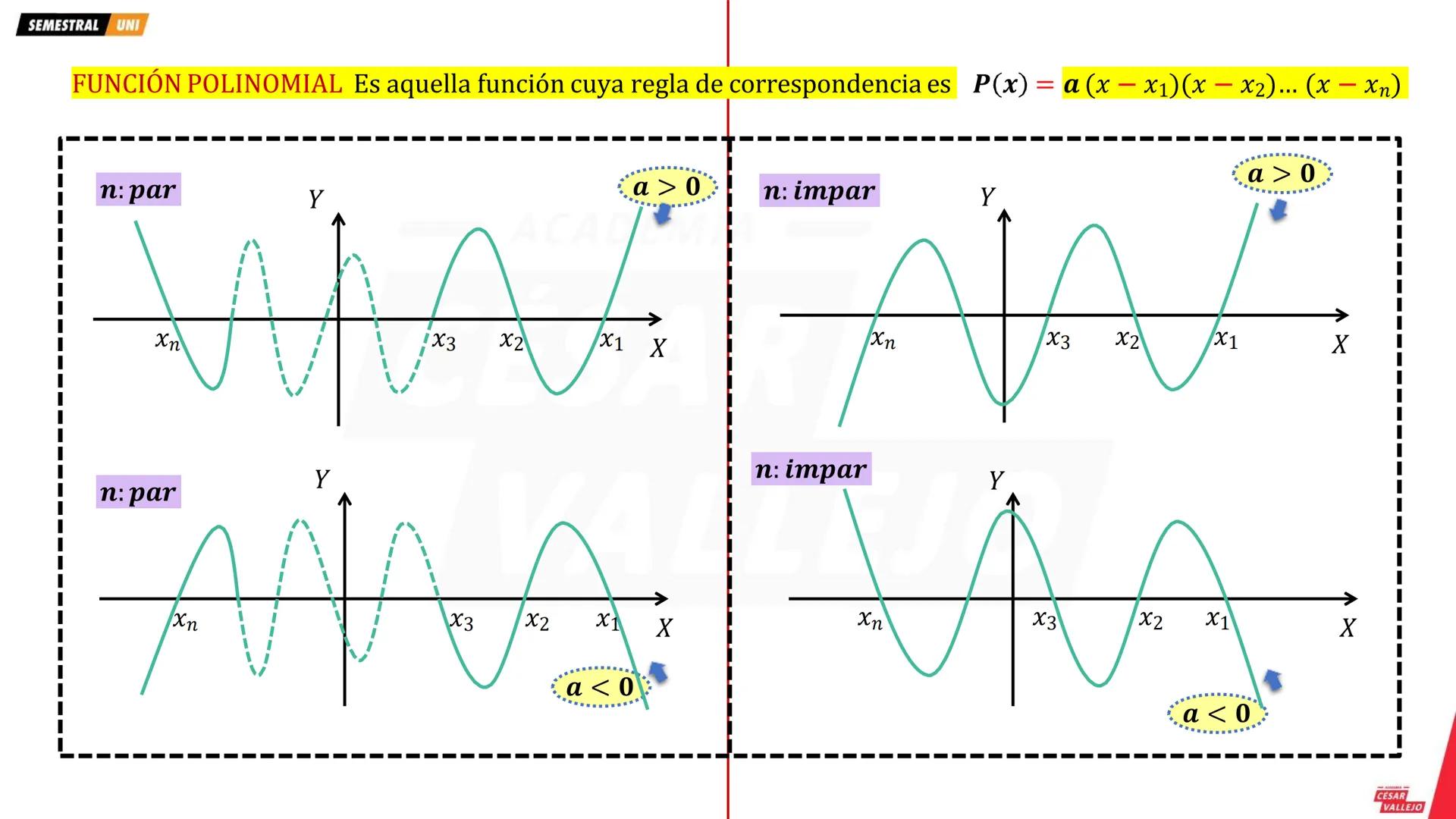
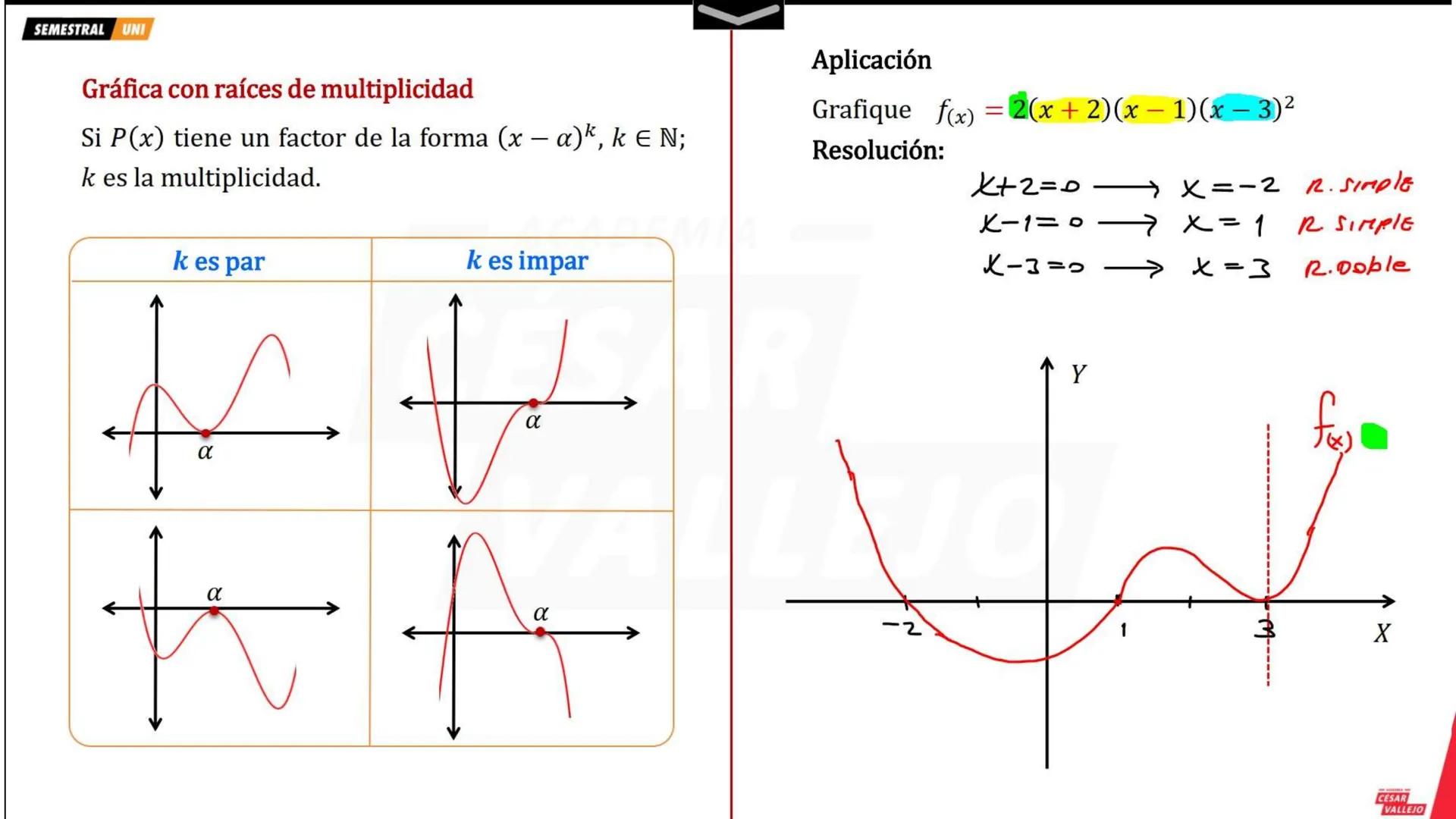
Función Cuadrática
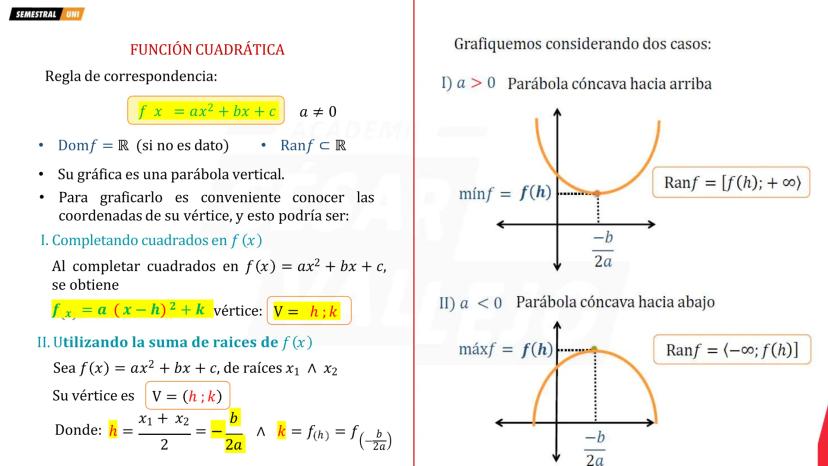
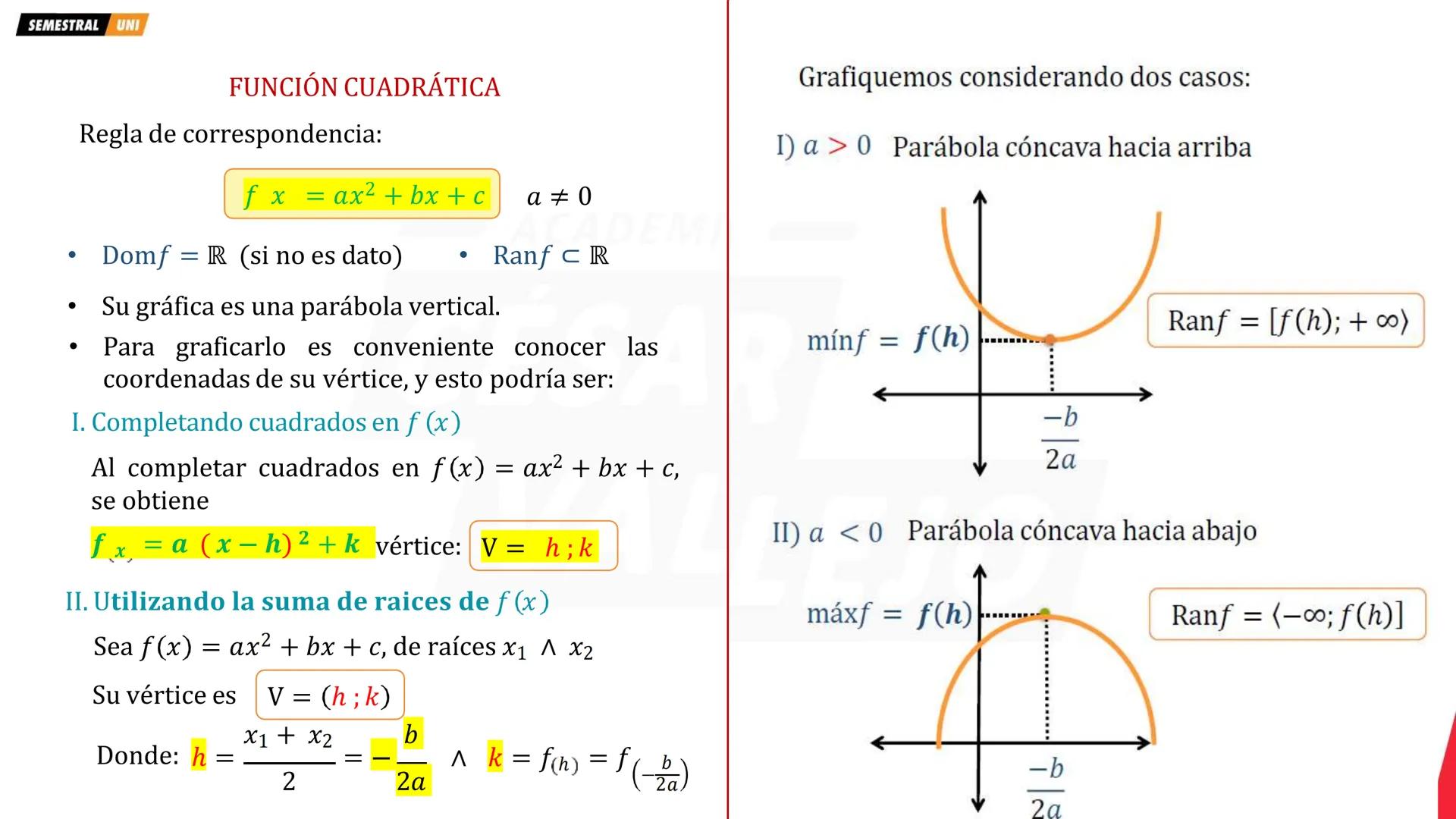
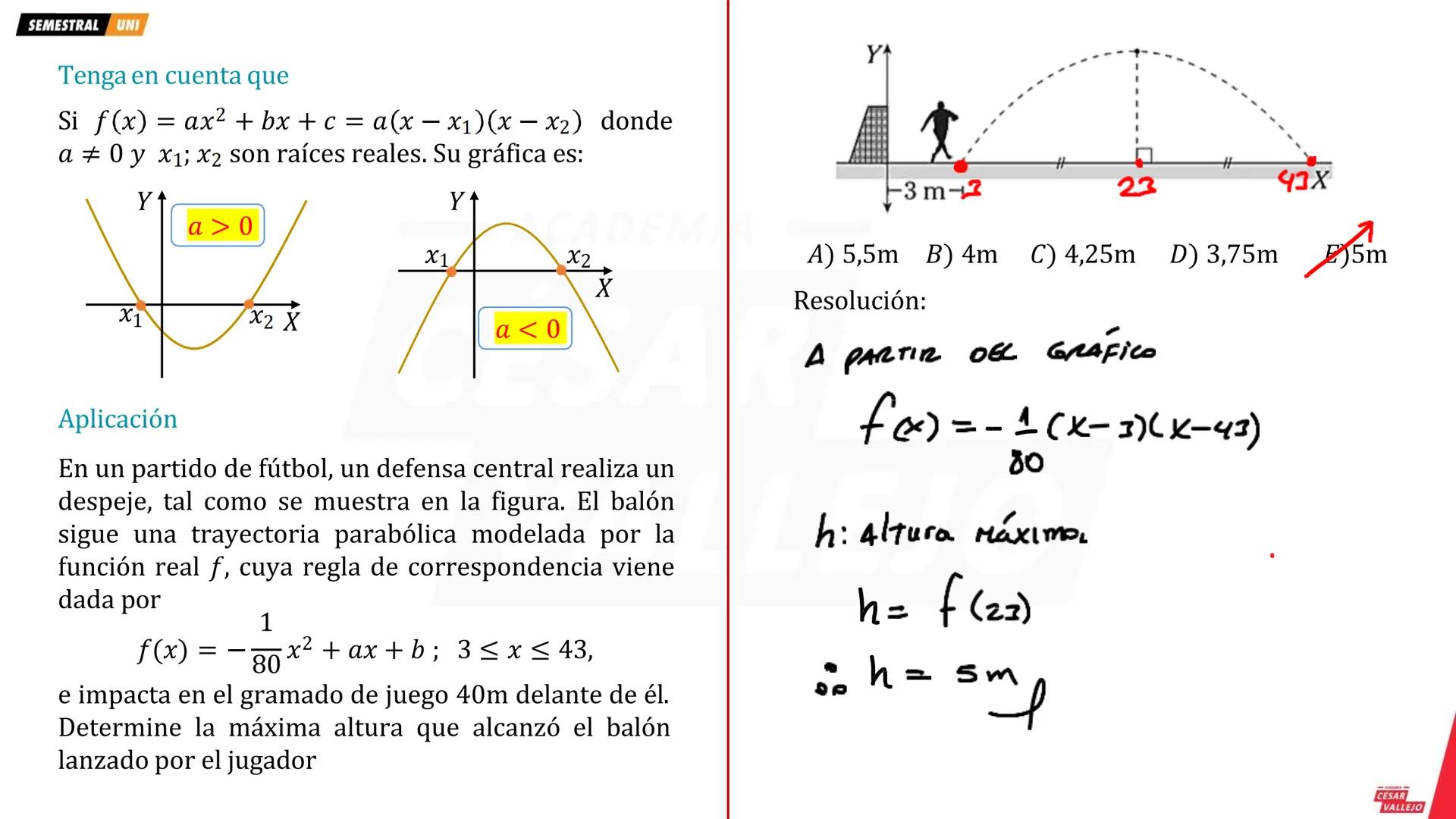
¿Alguna vez te preguntaste por qué las pelotas siguen esa curva perfecta cuando las lanzas? Esa es una función cuadrática en acción. Su forma general es f(x) = ax² + bx + c donde a ≠ 0.
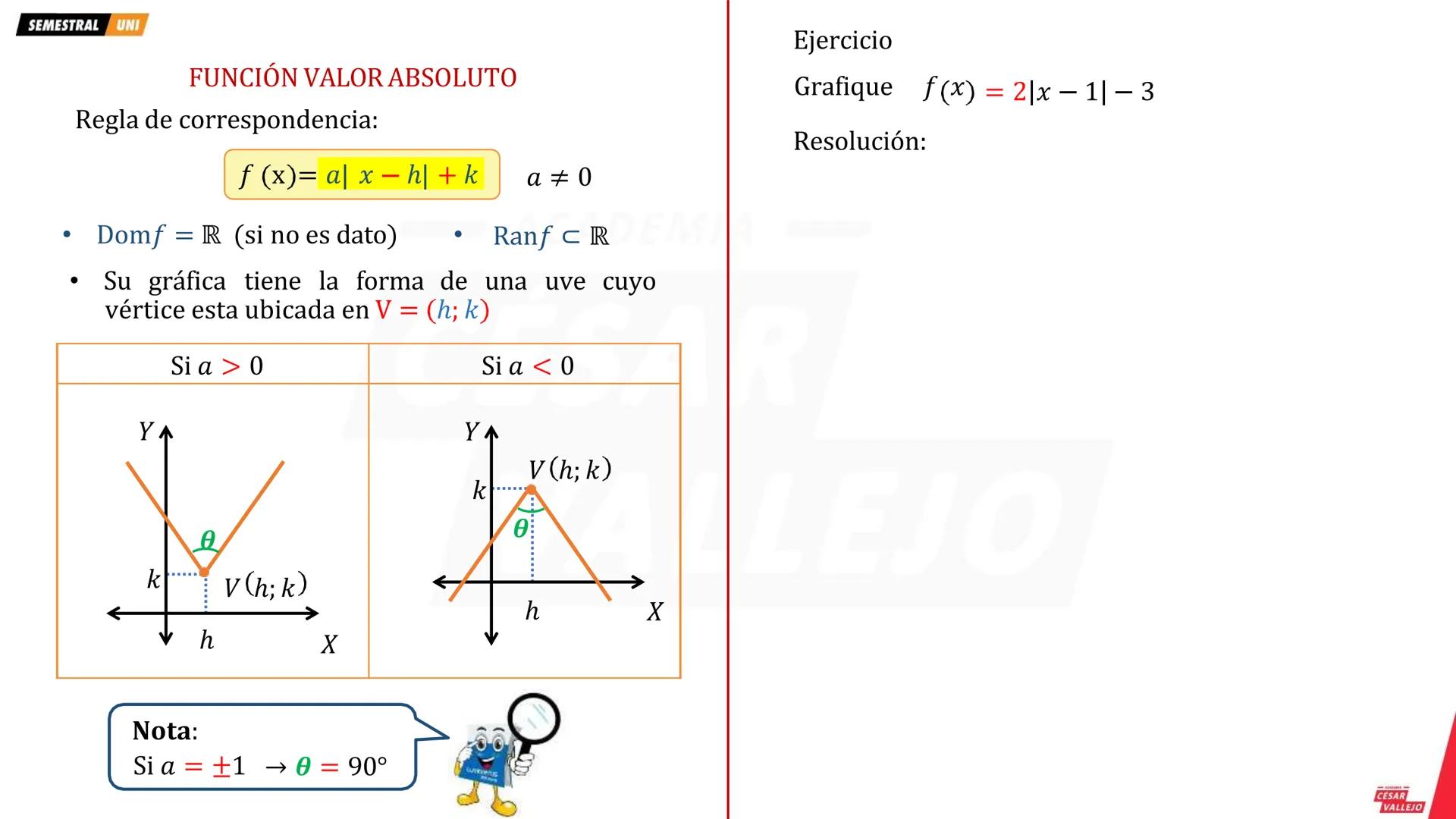
La clave para graficar está en encontrar el vértice V(h,k). Usa la fórmula h = -b/2a para la coordenada x, y luego k = f(h) para la coordenada y. Si a > 0, la parábola abre hacia arriba (tiene un valor mínimo). Si a < 0, abre hacia abajo (tiene un valor máximo).
El dominio siempre es todos los reales, pero el rango depende del vértice. Para a > 0: Rango = k,+∞).Paraa<0:Rango=(−∞,k.
Tip clave: Cuando tengas las raíces x₁ y x₂, el vértice está justo en el medio: h = x1+x2/2