Productos Trigonométricos y Valores Notables
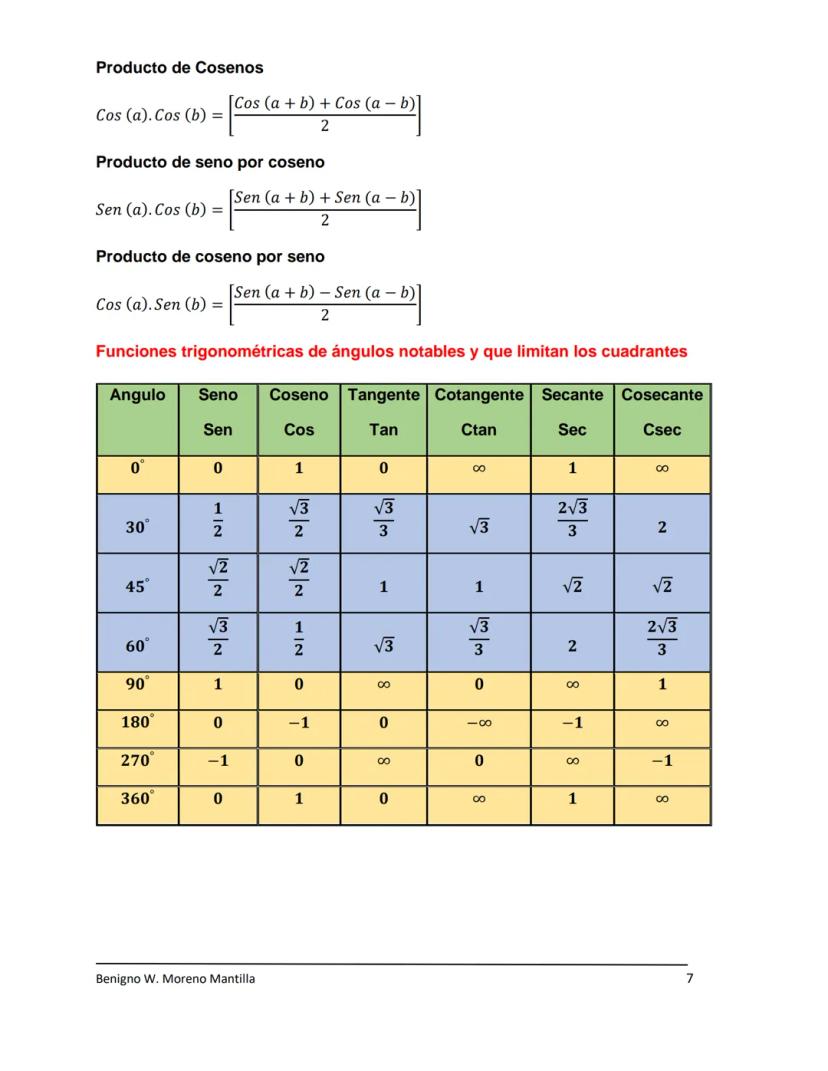
Los productos de funciones trigonométricas se pueden convertir en sumas, lo que facilita enormemente la integración. Estas transformaciones son clave para resolver integrales complicadas.
Las fórmulas de producto (sen·sen, cos·cos, sen·cos) siguen patrones específicos. Todas involucran promedios de ángulos: a+b/2 y a−b/2.
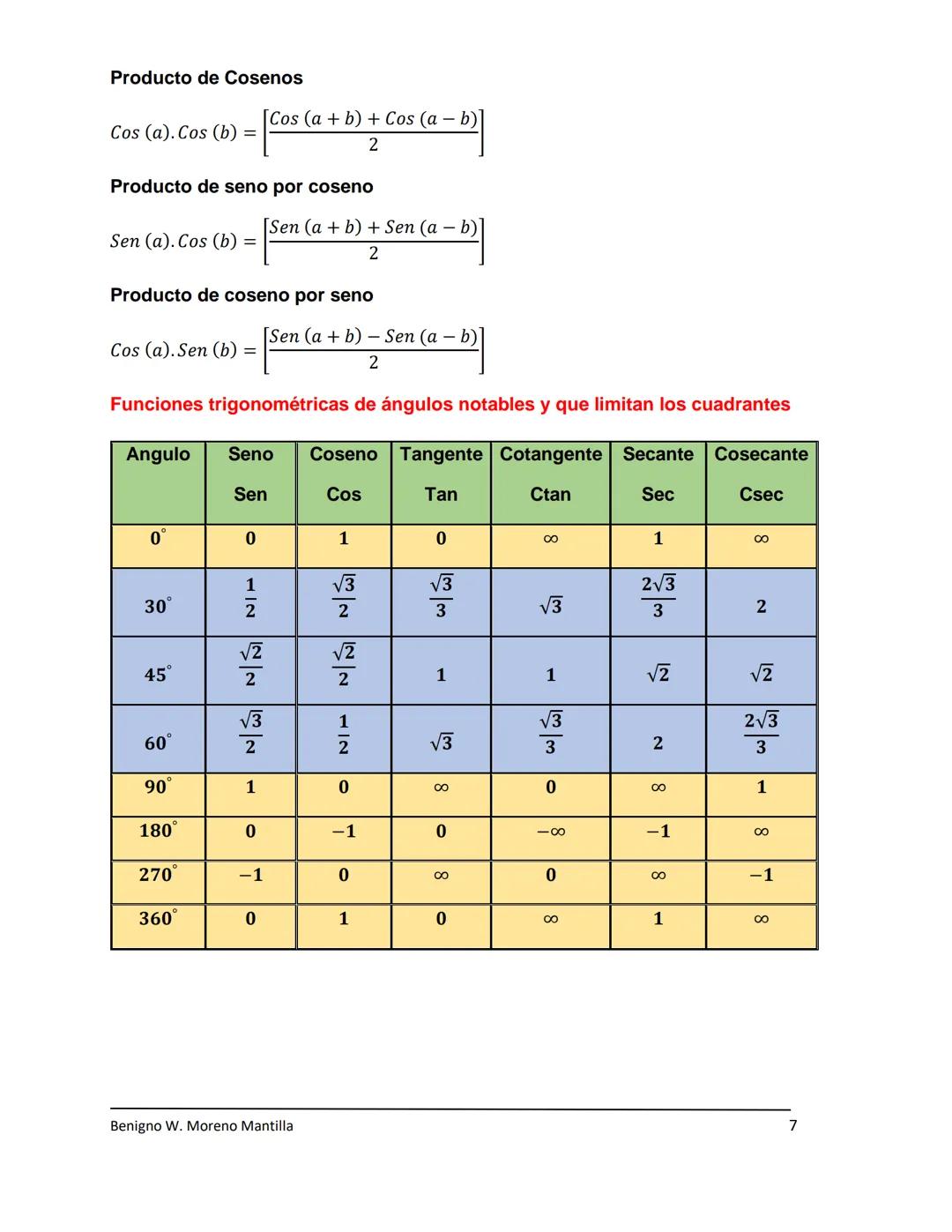
La tabla de valores notables es imprescindible - debes conocer los valores exactos para 0°, 30°, 45°, 60°, y 90°. Estos ángulos aparecen en casi todos los problemas de trigonometría.
Observa los patrones: para 30° y 60° los valores se "intercambian" entre seno y coseno. El ángulo de 45° tiene la particularidad de que sen(45°) = cos(45°) = √2/2.
Método de memoria: Para recordar valores notables, usa el patrón √0/2, √1/2, √2/2, √3/2, √4/2 para senos de 0°, 30°, 45°, 60°, 90°.