Definición de Circunferencia

Una circunferencia es el conjunto de todos los puntos de un plano que se encuentran a la misma distancia (equidistan) de un punto fijo llamado centro. Esta distancia constante se conoce como radio de la circunferencia.

Cuando veas una circunferencia, piensa en ella como una línea curva cerrada donde cualquier punto que traces sobre ella estará exactamente a la misma distancia del centro. Esta propiedad fundamental es lo que hace que la circunferencia sea una figura perfectamente simétrica.

💡 Recuerda que la circunferencia es solo la línea curva, mientras que el círculo incluye también el área interior.

Elementos de una Circunferencia

La circunferencia tiene varios elementos clave que debes conocer para resolver problemas geométricos:

El radio es el segmento que conecta el centro con cualquier punto de la circunferencia (como el segmento OP). Este es el valor que determina el tamaño de la circunferencia.

Una cuerda es cualquier segmento que une dos puntos de la circunferencia (como CD). El diámetro es un caso especial de cuerda que pasa por el centro (como AB) y siempre es el doble del radio.

El arco es una porción de la circunferencia delimitada por dos puntos (como el arco CD). Los arcos son importantes para calcular ángulos y medidas en problemas de geometría.

Relación entre Rectas y Circunferencias

Existen distintas formas en que una recta puede relacionarse con una circunferencia:

Una recta secante intersecta a la circunferencia en exactamente dos puntos (como Ls). Esto crea dos arcos en la circunferencia y divide el plano.

Una recta tangente toca la circunferencia en un único punto llamado punto de tangencia (como LT). Esta recta es especialmente importante en problemas de construcciones geométricas.

La flecha o sagita es la parte del radio perpendicular a una cuerda que va desde la cuerda hasta la circunferencia (como MH). Este elemento nos ayuda a calcular distancias entre cuerdas y el centro.

🔍 ¡Atención! La recta tangente siempre forma un ángulo de 90° con el radio en el punto de tangencia.

Teorema del Diámetro Perpendicular

Un teorema fundamental que te ayudará a resolver muchos problemas es: En una circunferencia, un diámetro perpendicular a una cuerda, biseca a ésta cuerda.

Esto significa que si trazas un diámetro que sea perpendicular a cualquier cuerda (como OC perpendicular a AB), este diámetro dividirá la cuerda en dos partes exactamente iguales $AH = BH$.

La demostración se basa en que el triángulo AOB es isósceles, por lo que OH actúa como mediana y divide a AB en segmentos congruentes. Esta propiedad es útil para encontrar distancias y construir figuras simétricas.

Puedes usar este teorema para resolver problemas de construcción o para hallar puntos medios en figuras que involucran circunferencias.

Recta Tangente y Radio

Un teorema esencial establece que: En una circunferencia, una recta tangente es perpendicular al radio trazado por el punto de tangencia.

Si L es una recta tangente a una circunferencia y P es el punto donde esta recta toca a la circunferencia (punto de tangencia), entonces el radio OP forma un ángulo recto (90°) con la recta L.

Esta propiedad es fundamental para muchos problemas de geometría, especialmente cuando necesitas calcular ángulos o distancias relacionadas con tangentes.

💡 Este teorema también funciona en sentido inverso: si una recta es perpendicular a un radio en su extremo sobre la circunferencia, entonces esa recta es tangente a la circunferencia.

Rectas Secantes y Tangentes

Cuando una circunferencia es tangente a dos rectas secantes, se cumple un teorema interesante: los segmentos determinados son congruentes.

Si una circunferencia toca dos rectas que se cortan en un punto P, y los puntos de tangencia son A y B, entonces los segmentos PA y PB tienen exactamente la misma longitud.

Para demostrarlo, analizamos los triángulos PAO y PBO, que resultan congruentes por el criterio Lado-Lado-Ángulo (LLA). Esta congruencia nos lleva a concluir que PA ≅ PB.

Esta propiedad tiene aplicaciones prácticas en problemas de tangencia y distancias, permitiéndote encontrar longitudes desconocidas cuando trabajas con circunferencias y rectas secantes.

Bisectriz y Centro de la Circunferencia

Cuando una circunferencia es tangente a dos rectas secantes, existe otra propiedad importante: la bisectriz de uno de los ángulos determinados por las rectas contiene al centro de la circunferencia.

Si una circunferencia toca a dos rectas secantes en los puntos A y B, y estas rectas se cortan en el punto P, entonces la recta que pasa por P y el centro O de la circunferencia actúa como bisectriz del ángulo APB.

La demostración se basa en que los triángulos PAO y PBO son congruentes (por el criterio LLA), lo que nos lleva a concluir que ∠APO = ∠BPO, confirmando que PO es efectivamente la bisectriz del ángulo APB.

🔍 Este teorema es muy útil para localizar el centro de una circunferencia cuando solo conoces los puntos de tangencia con dos rectas.

Medida de Arcos y Ángulos

La medida de un arco de circunferencia está directamente relacionada con el ángulo central que lo determina: la medida de un arco es igual a la medida del ángulo determinado por los radios trazados por los extremos del arco.

Si α es la medida del arco AB y θ es la medida del ángulo AOB formado por los radios OA y OB, entonces α = θ. Esta relación fundamental nos permite calcular longitudes de arco conociendo ángulos, o viceversa.

Esta propiedad es esencial para resolver problemas que involucran sectores circulares, segmentos y ángulos inscritos en una circunferencia.

Recuerda que cuando expresamos la medida en radianes, podemos relacionarla directamente con la longitud del arco mediante la fórmula: longitud del arco = radio × medida del ángulo en radianes.

Cuerdas y Arcos Congruentes

Un teorema clave establece que: Si en una circunferencia se trazan dos cuerdas congruentes, entonces los arcos que subtienden estas cuerdas son congruentes.

Esto significa que si tienes dos cuerdas de la misma longitud (AB ≅ CD), entonces los arcos que se forman sobre ellas también tendrán la misma medida (arco AB ≅ arco CD).

La demostración se realiza comprobando que los triángulos AOB y COD son congruentes (por el criterio LLL), lo que hace que sus ángulos correspondientes también sean congruentes (∠AOB ≅ ∠COD). Y como la medida del arco es igual a la medida del ángulo central, los arcos resultan congruentes.

💡 Este teorema también funciona en sentido inverso: si dos arcos son congruentes, las cuerdas que los subtienden también lo son.

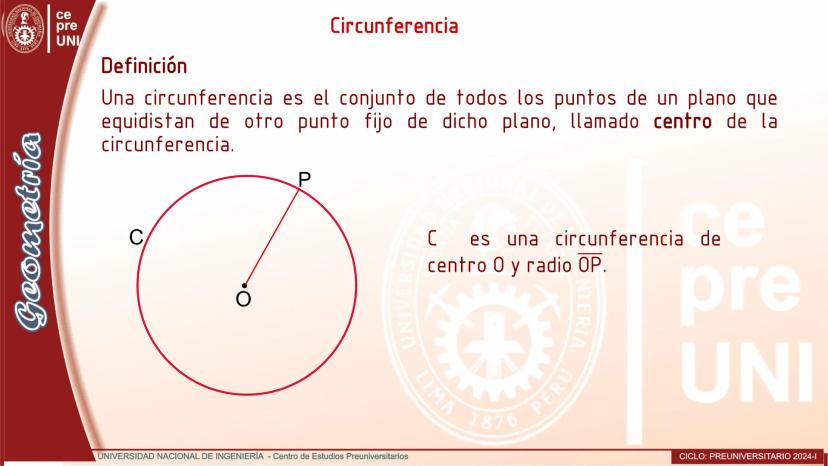
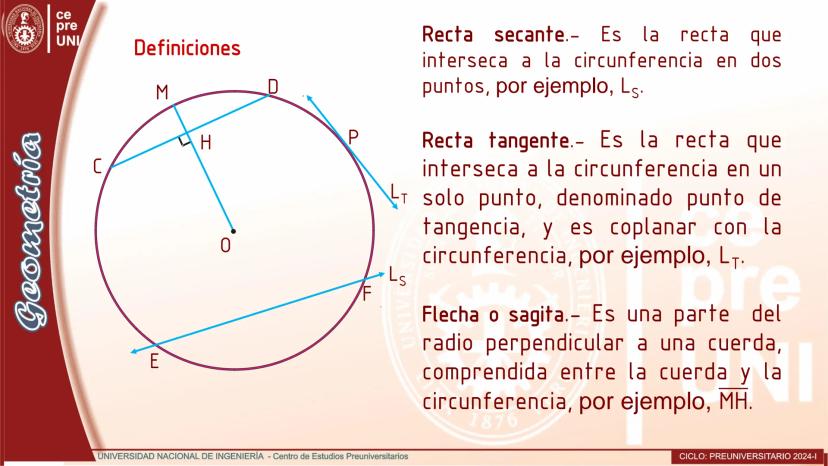
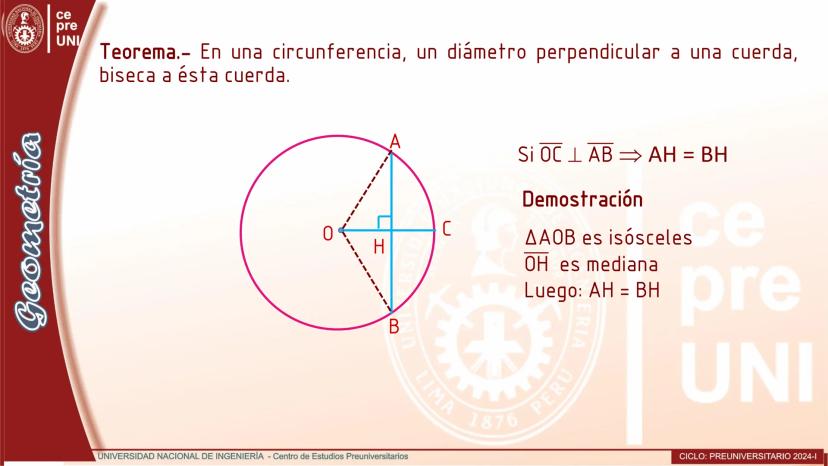
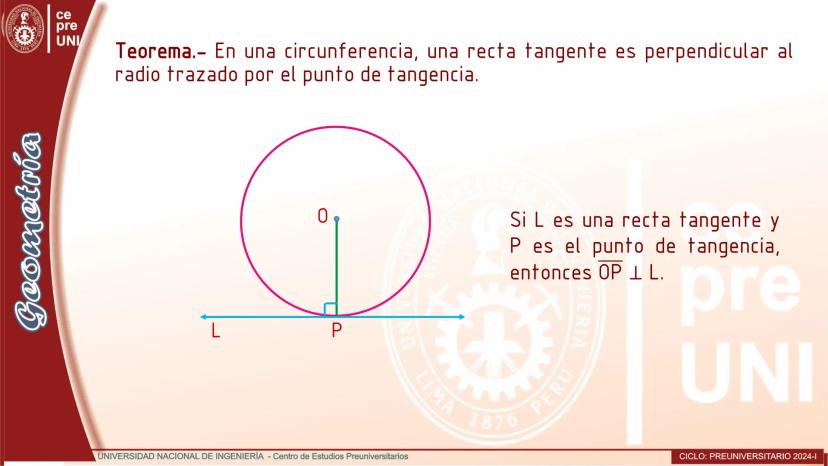
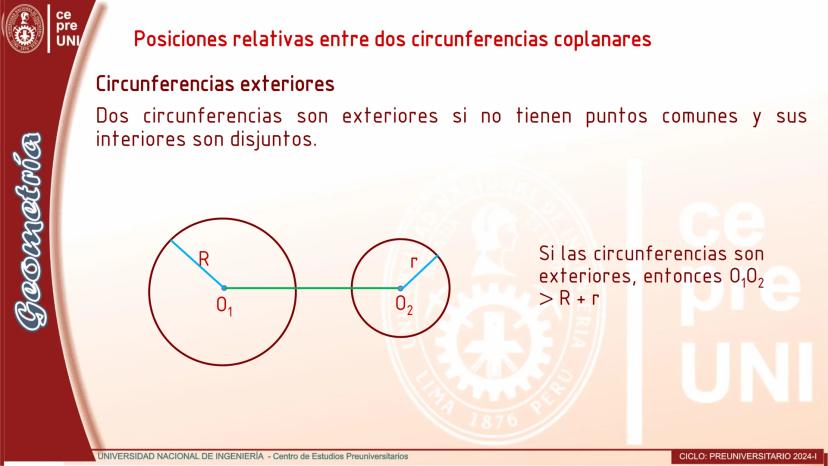
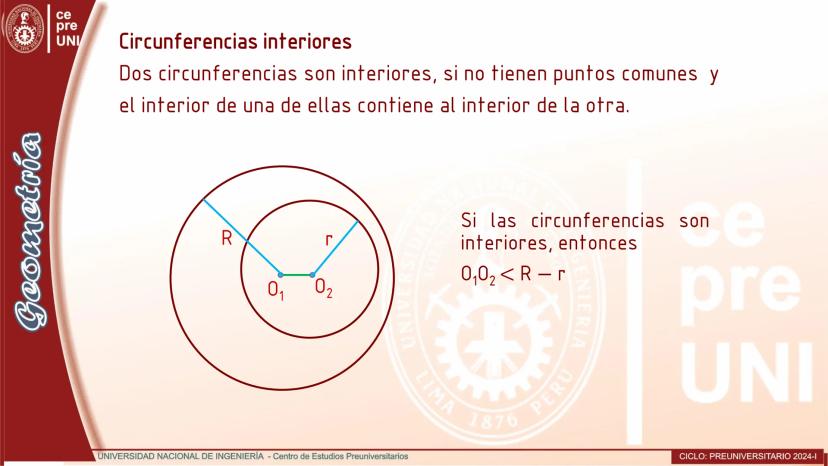
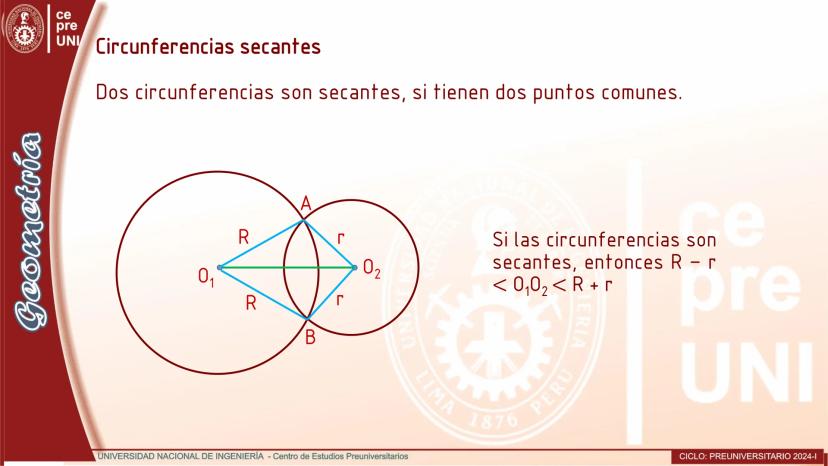
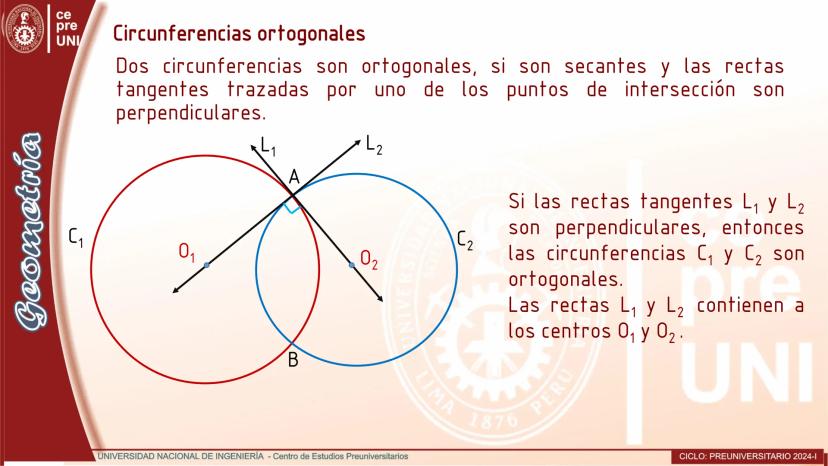
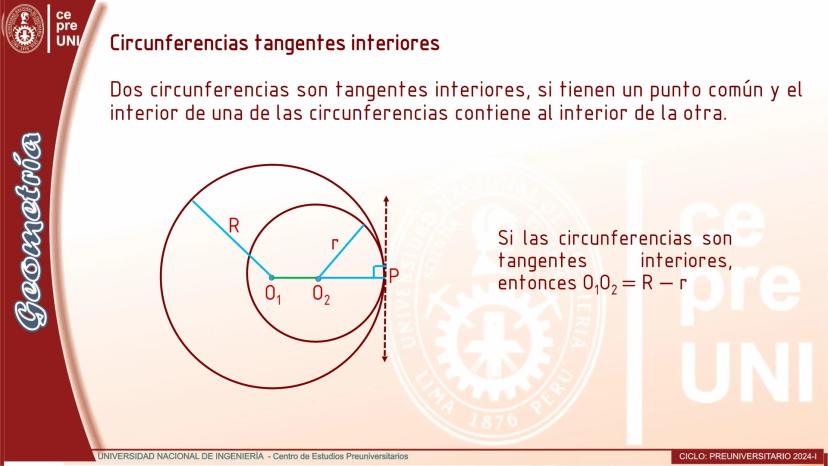
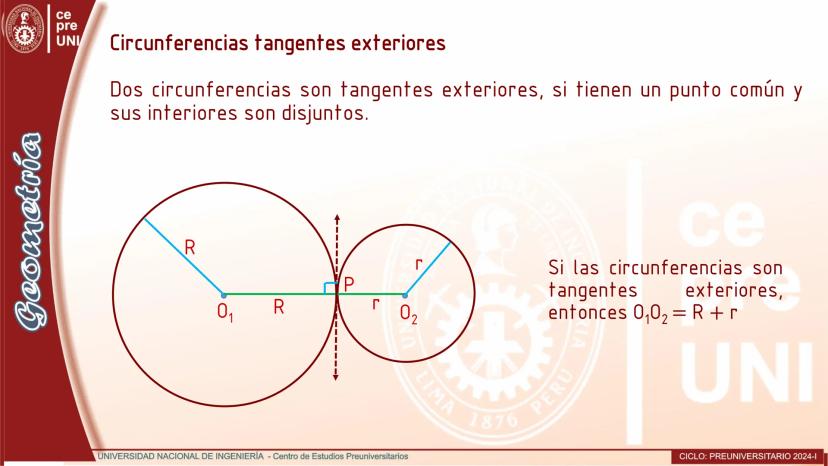
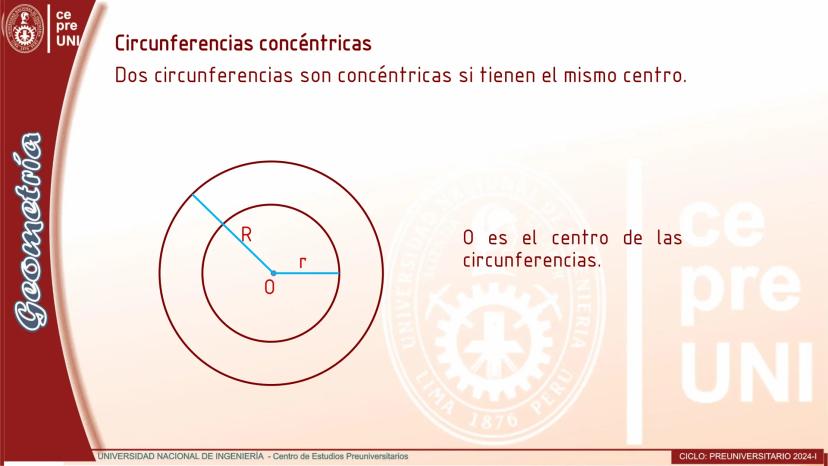
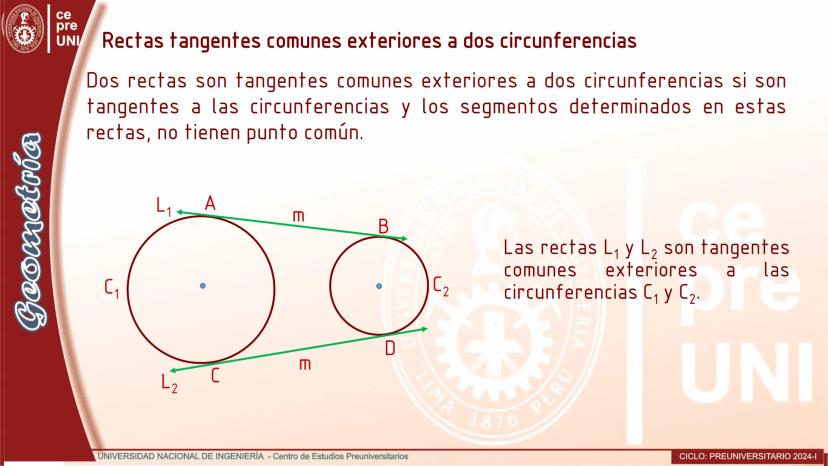
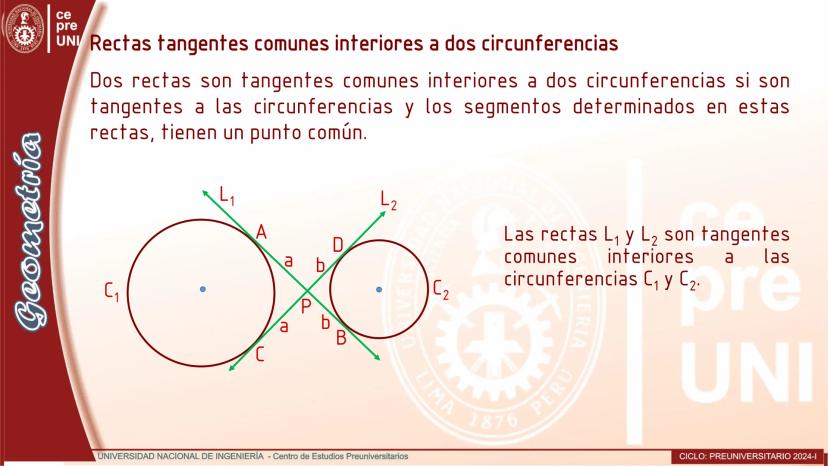
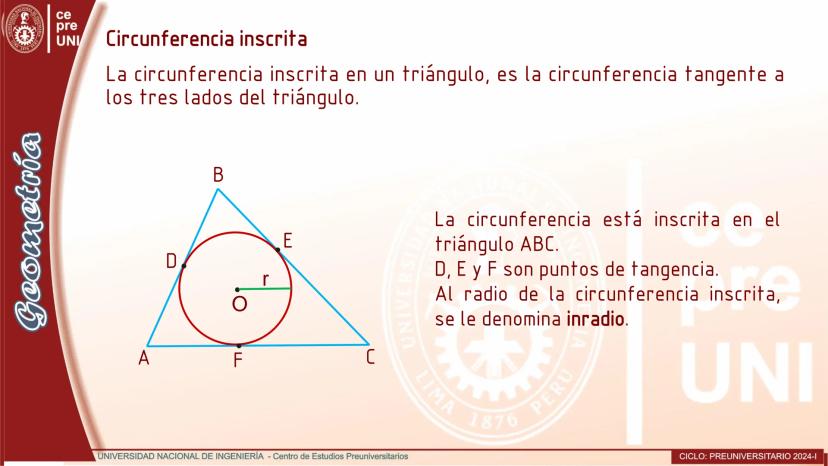
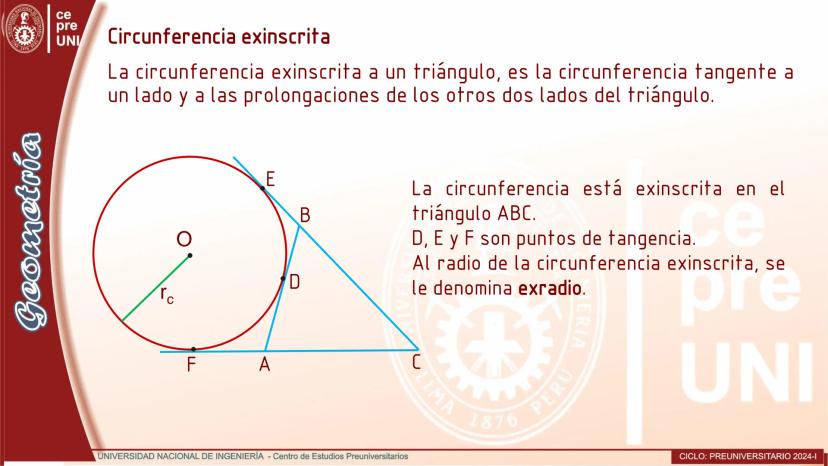
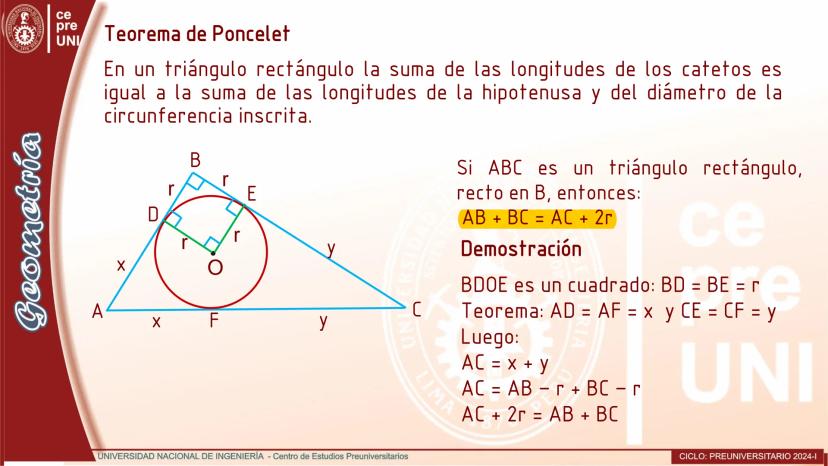
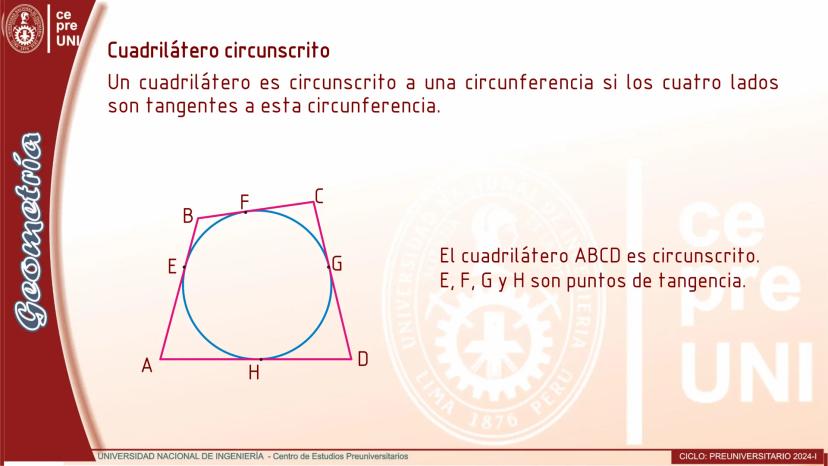
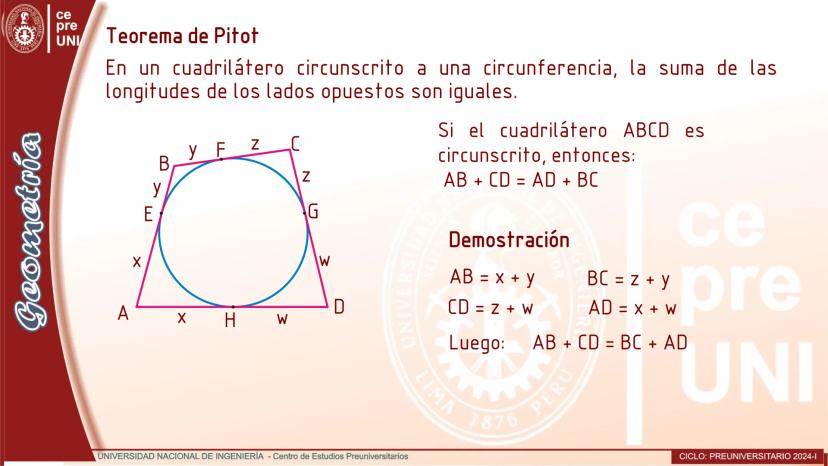
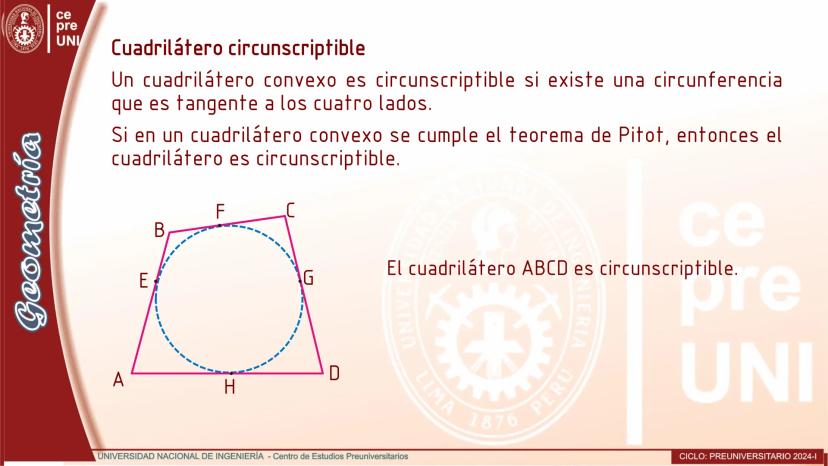
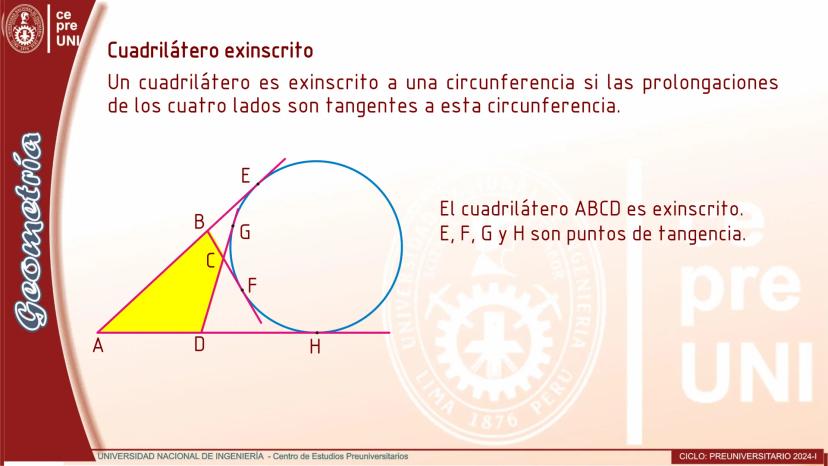
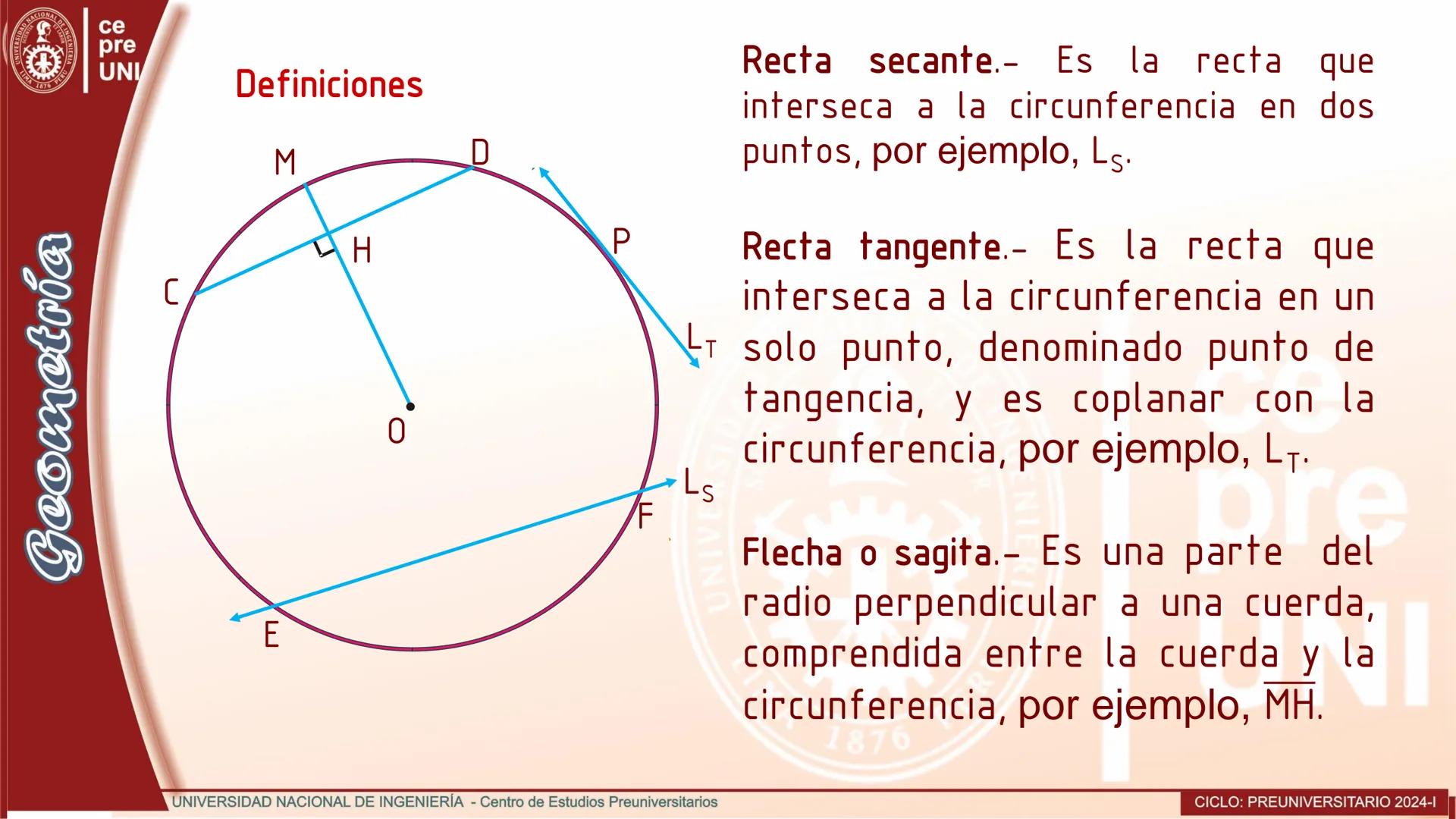
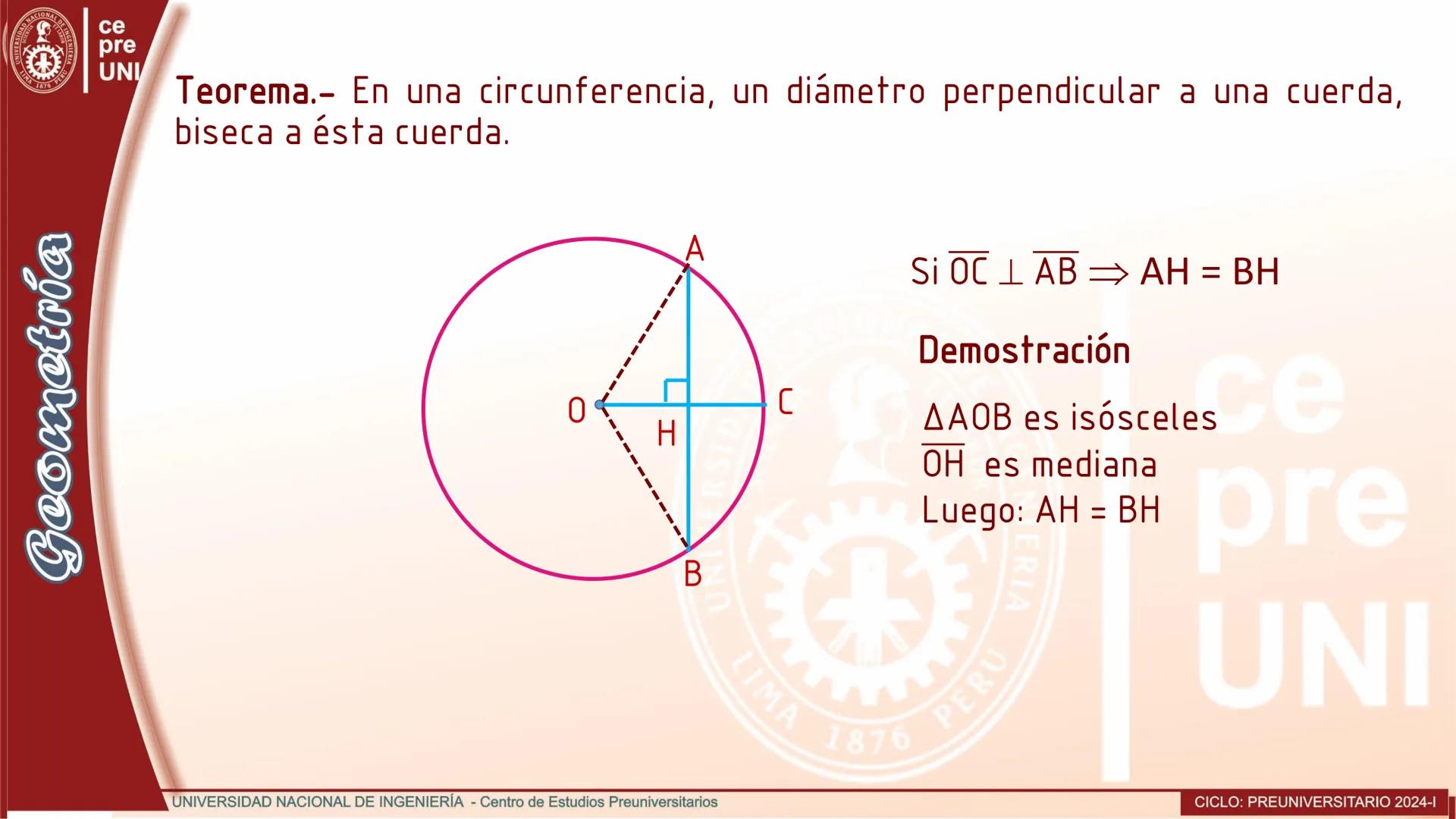
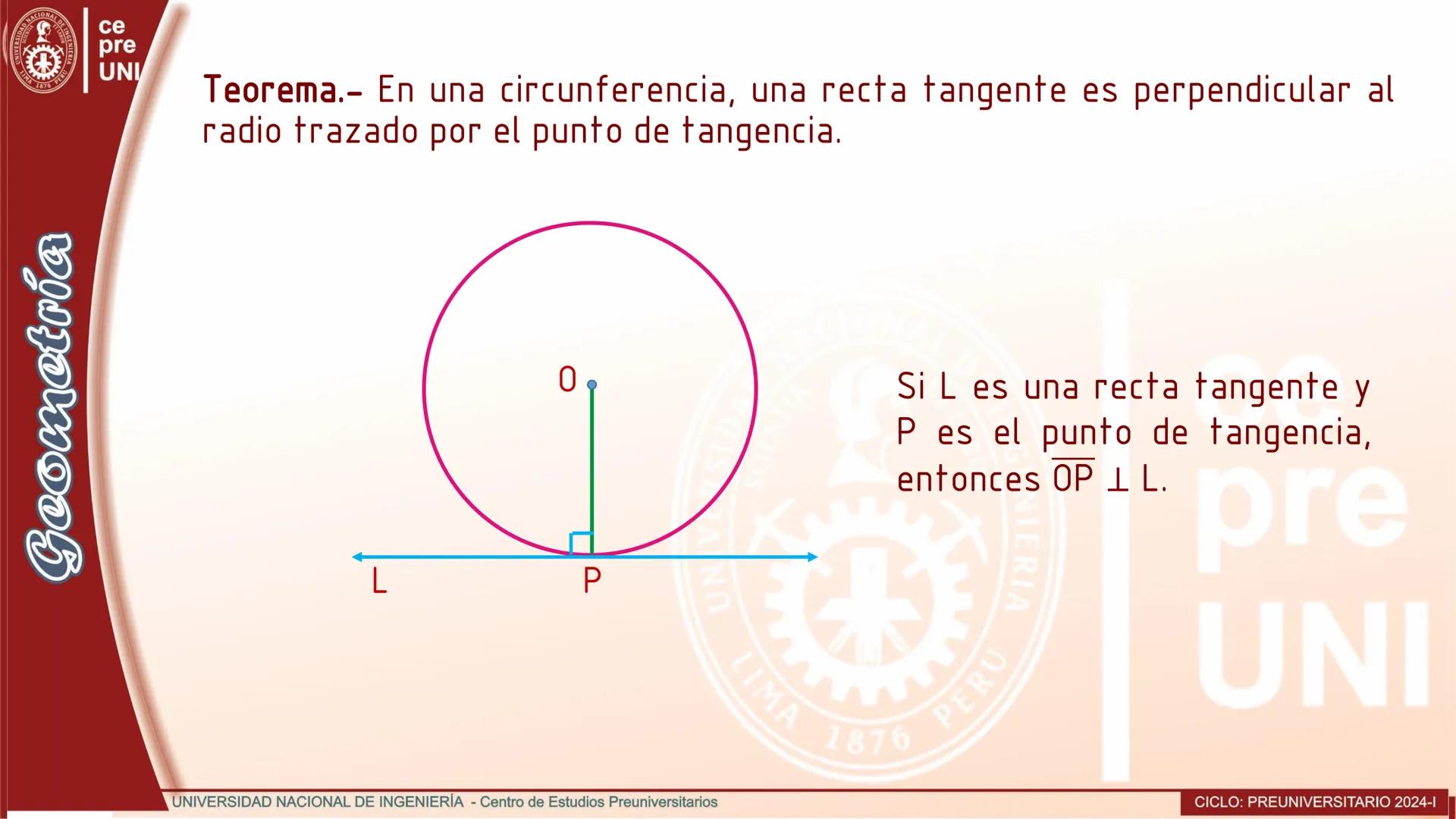
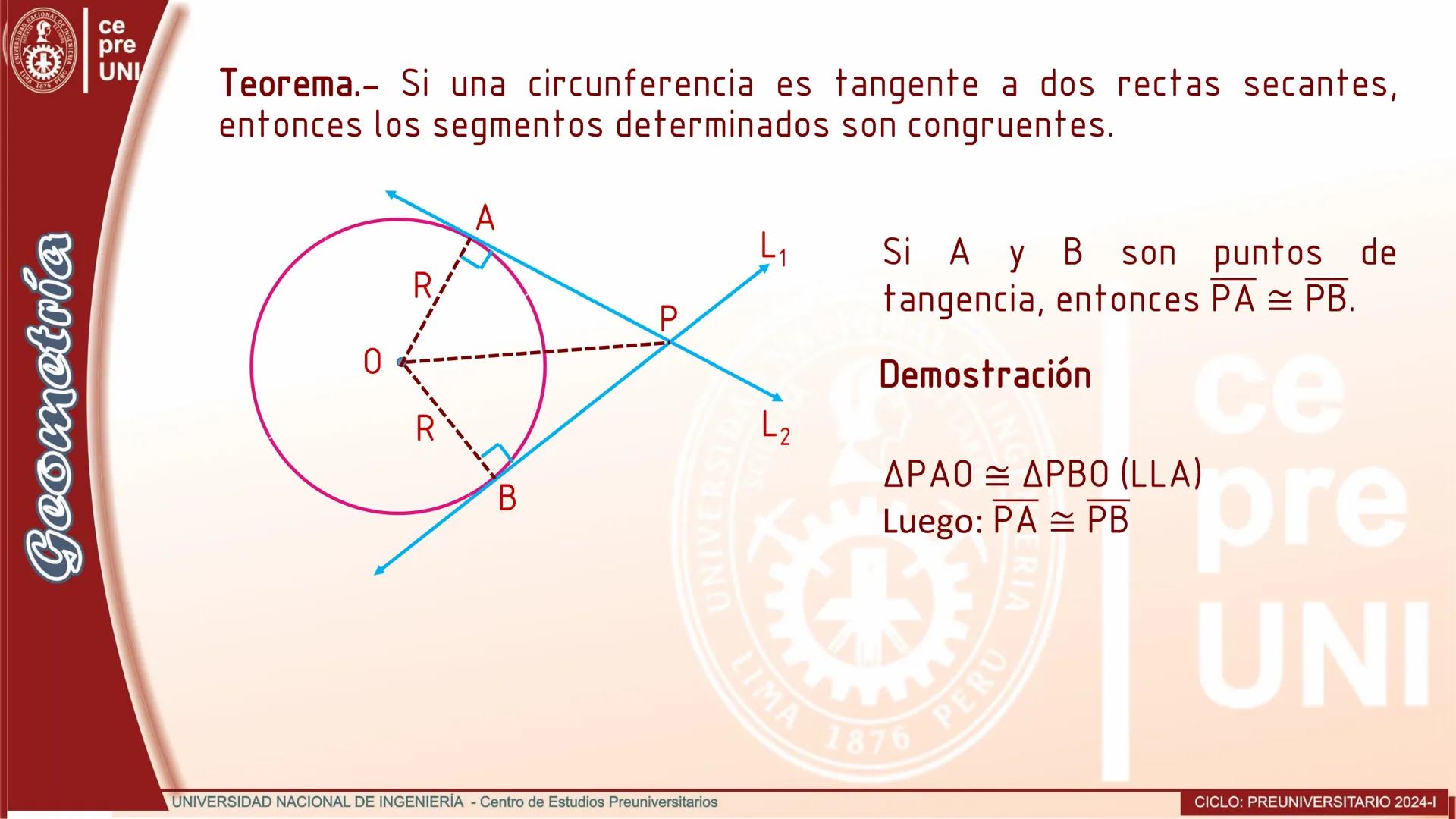
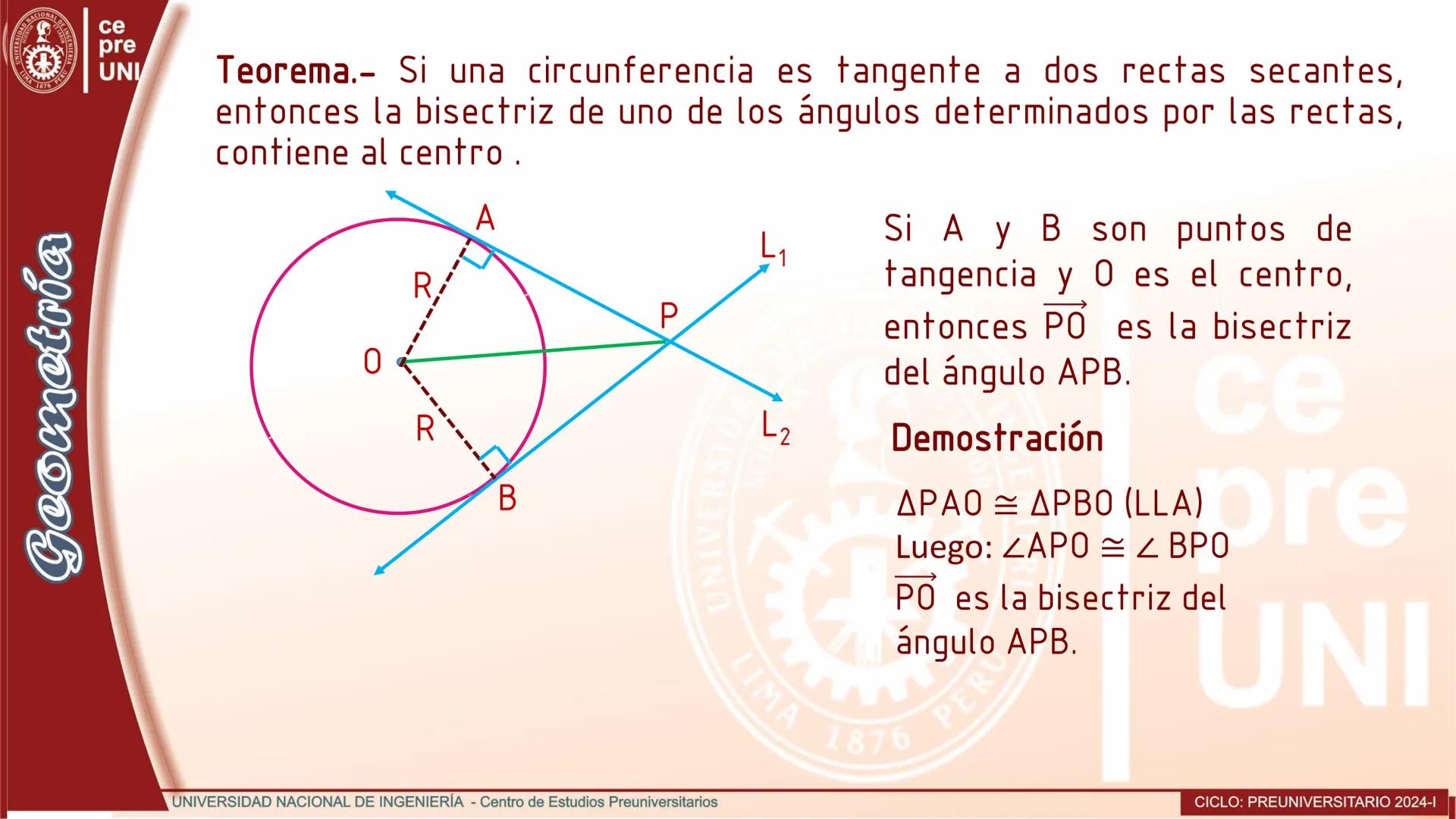
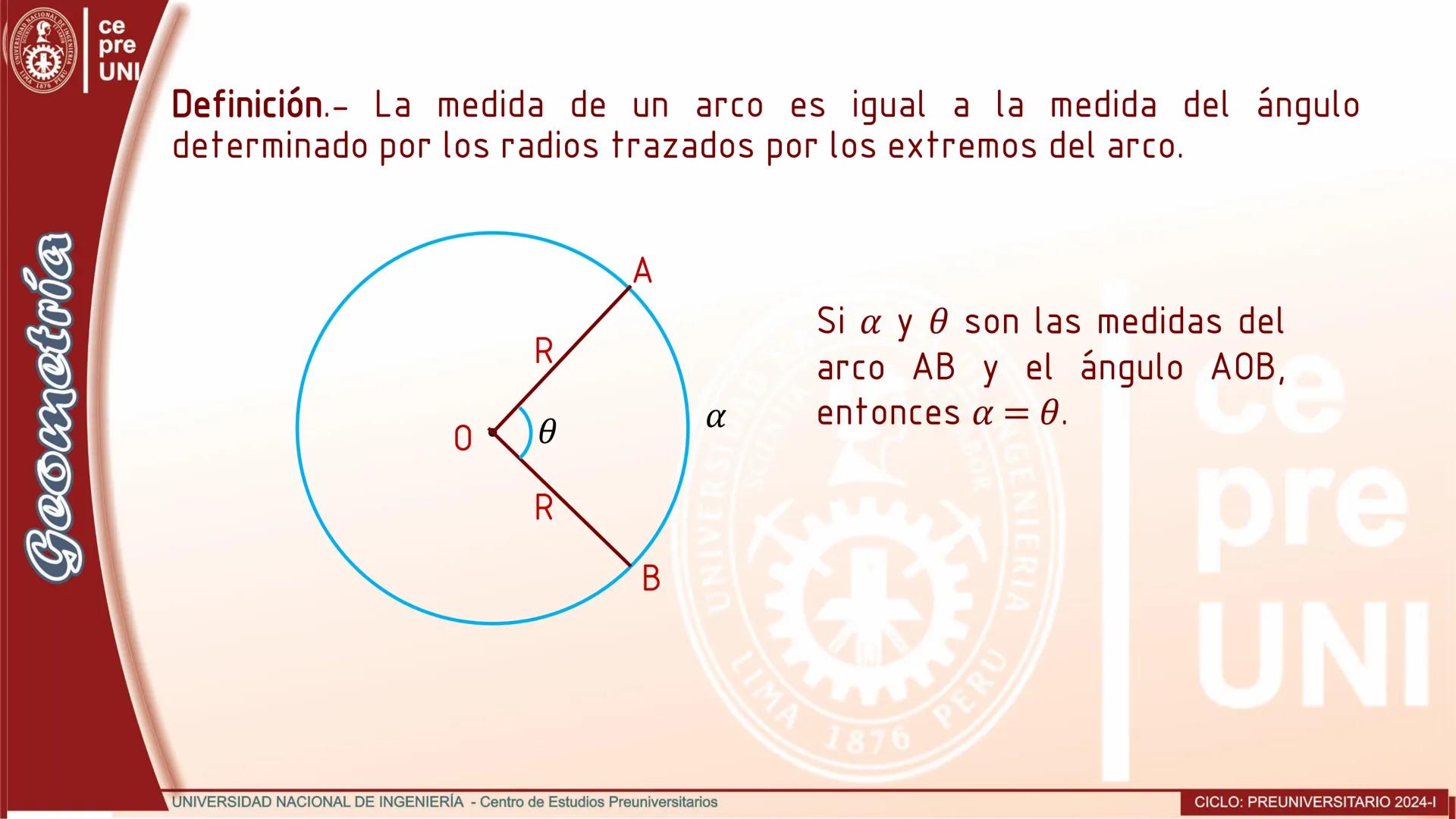
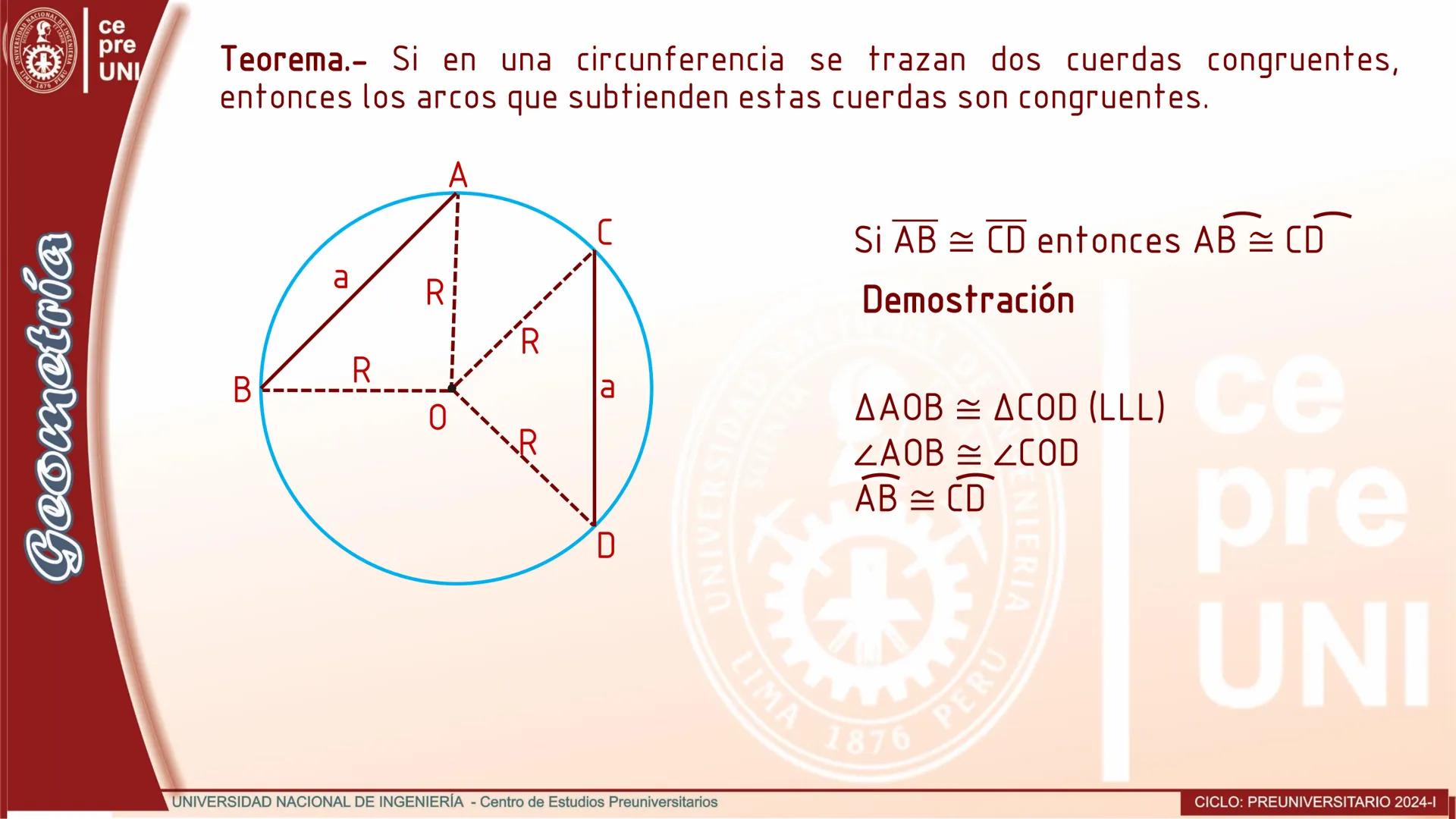
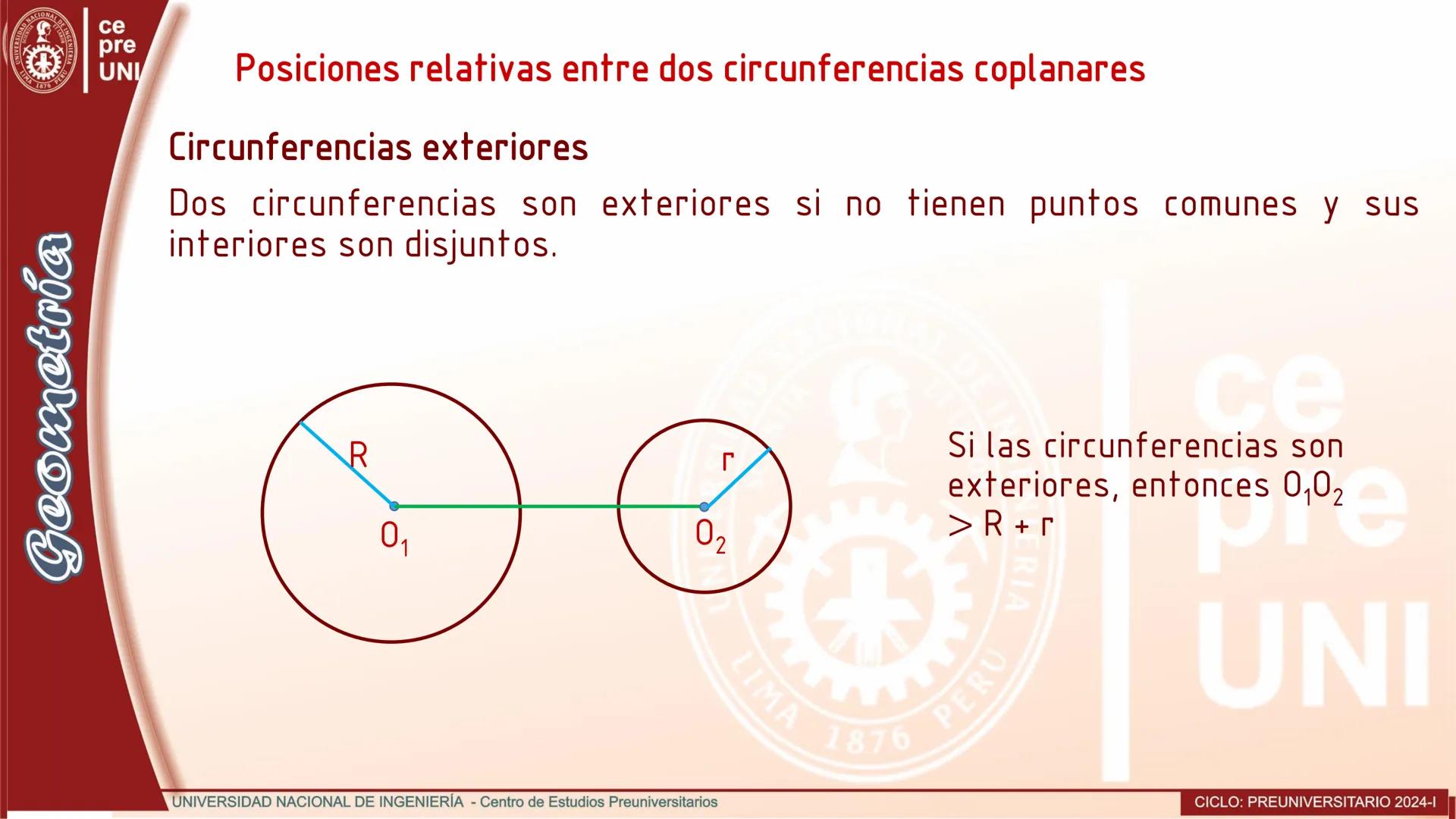
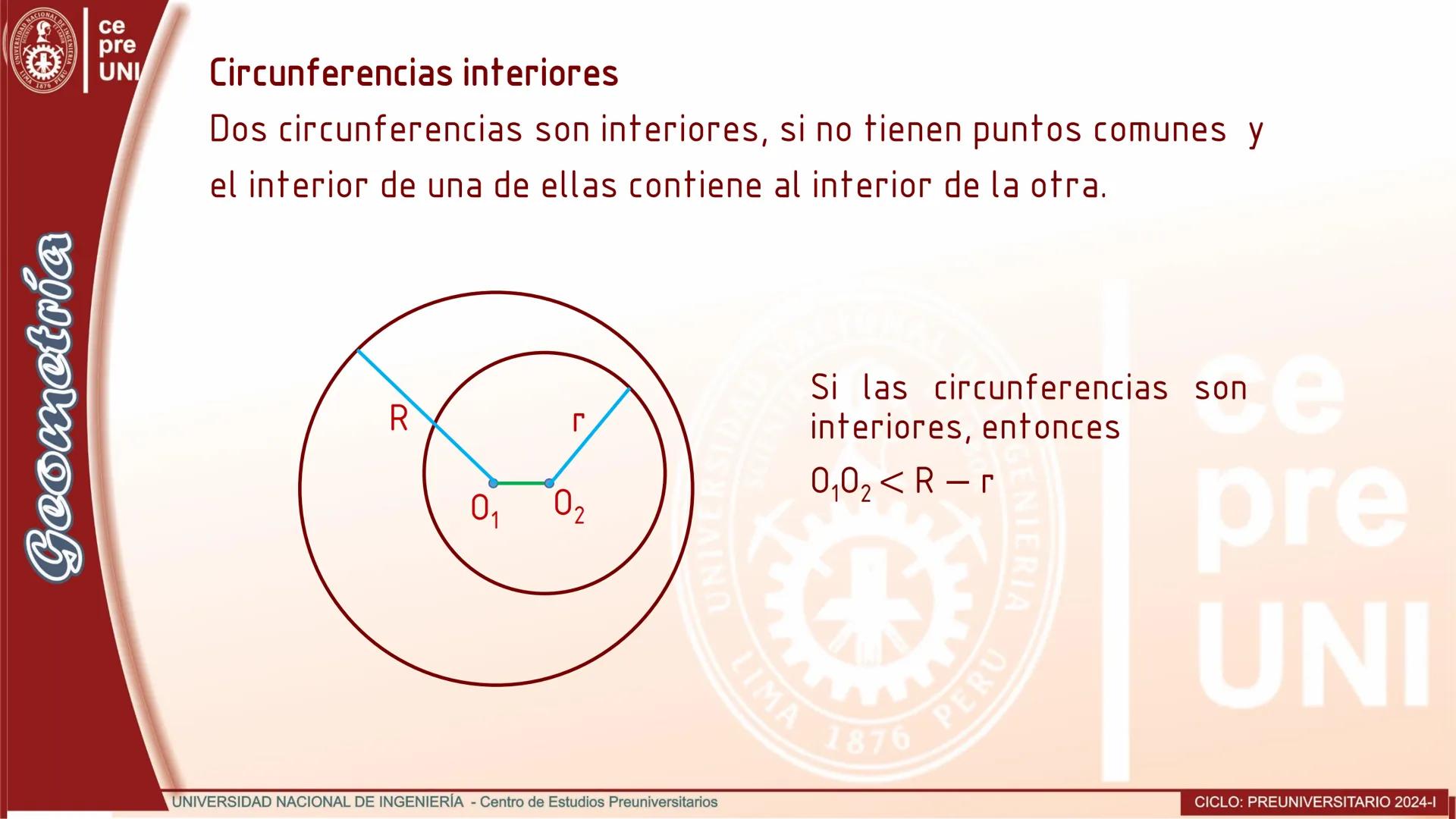
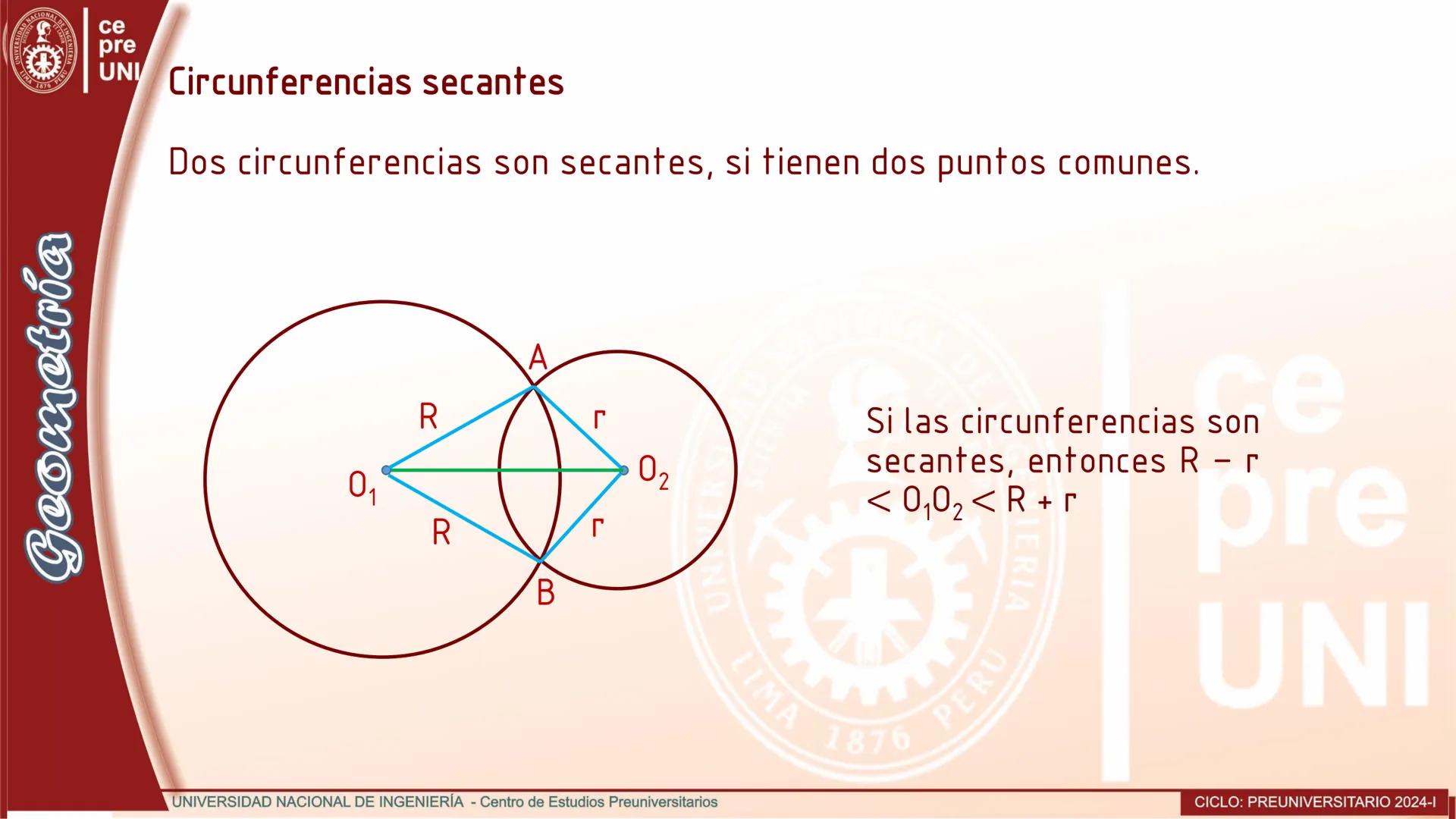
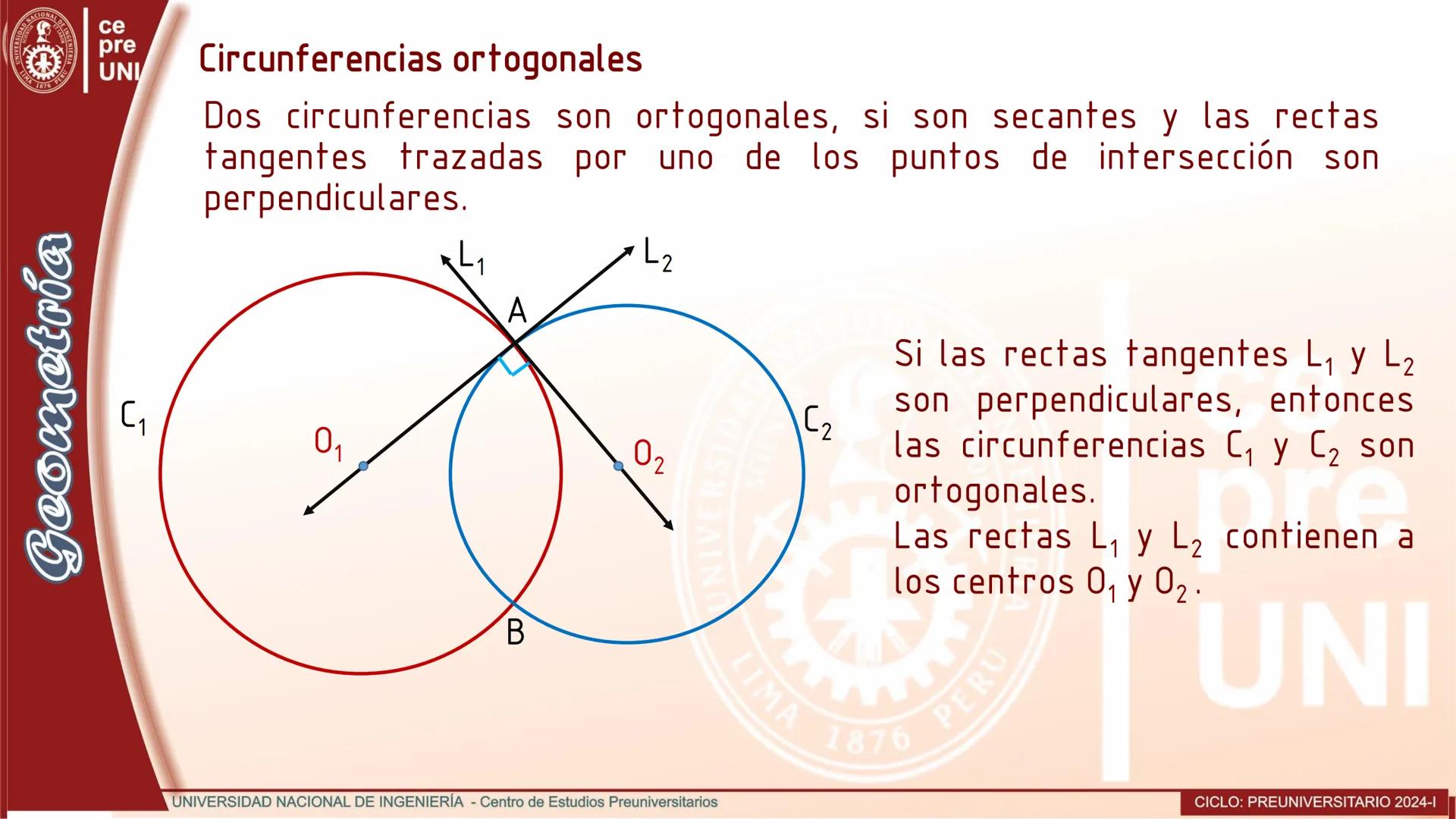
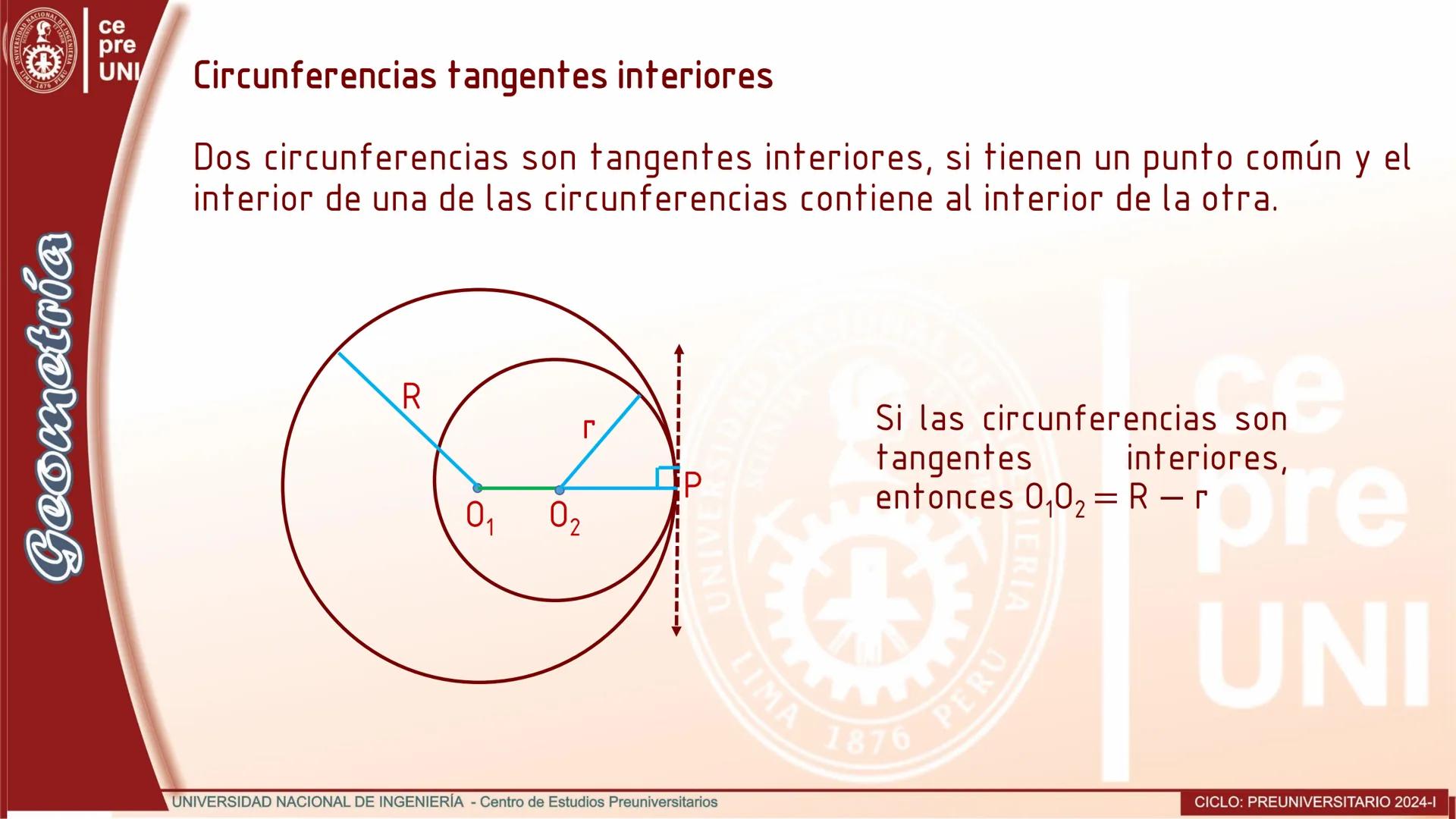
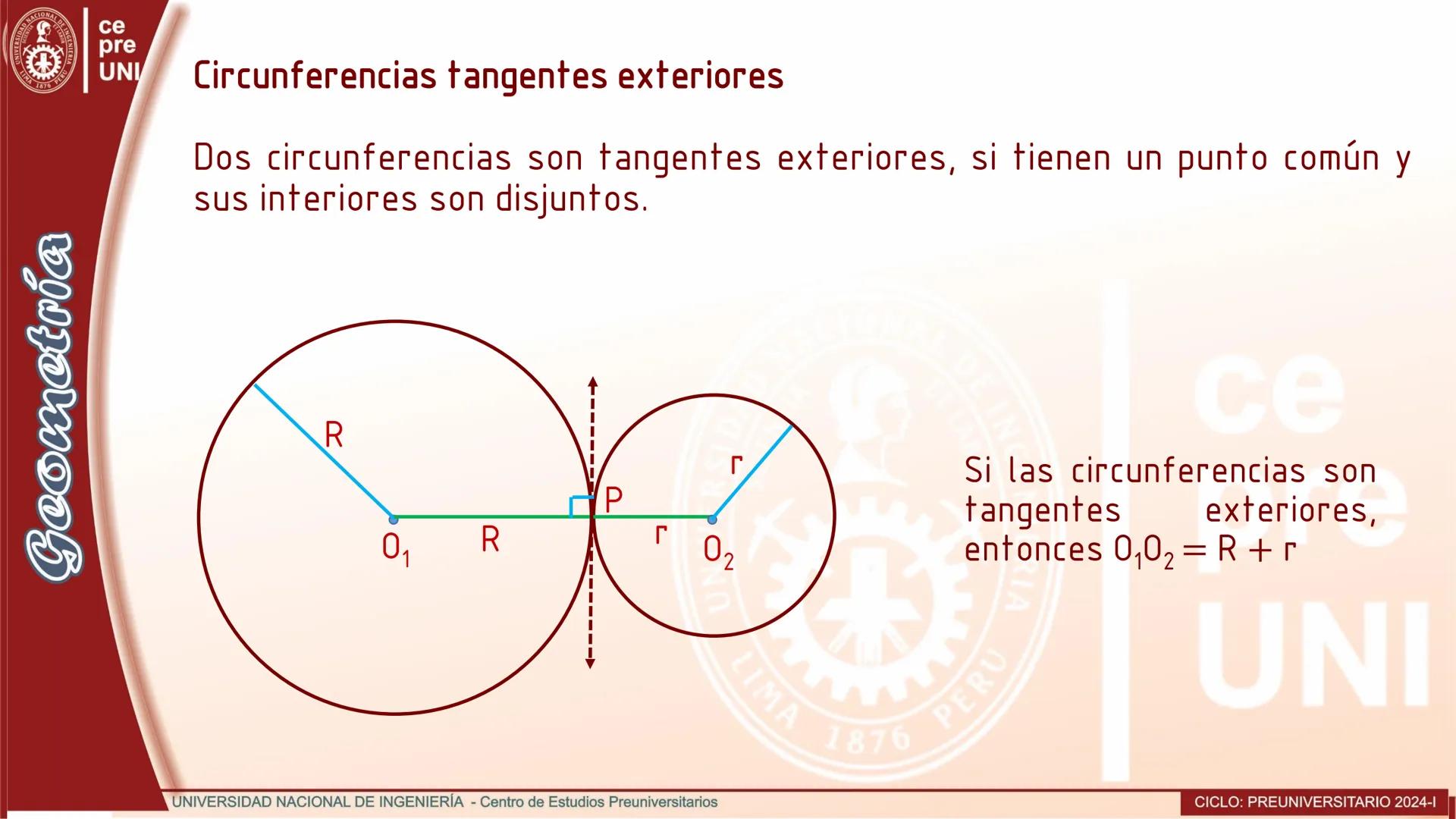
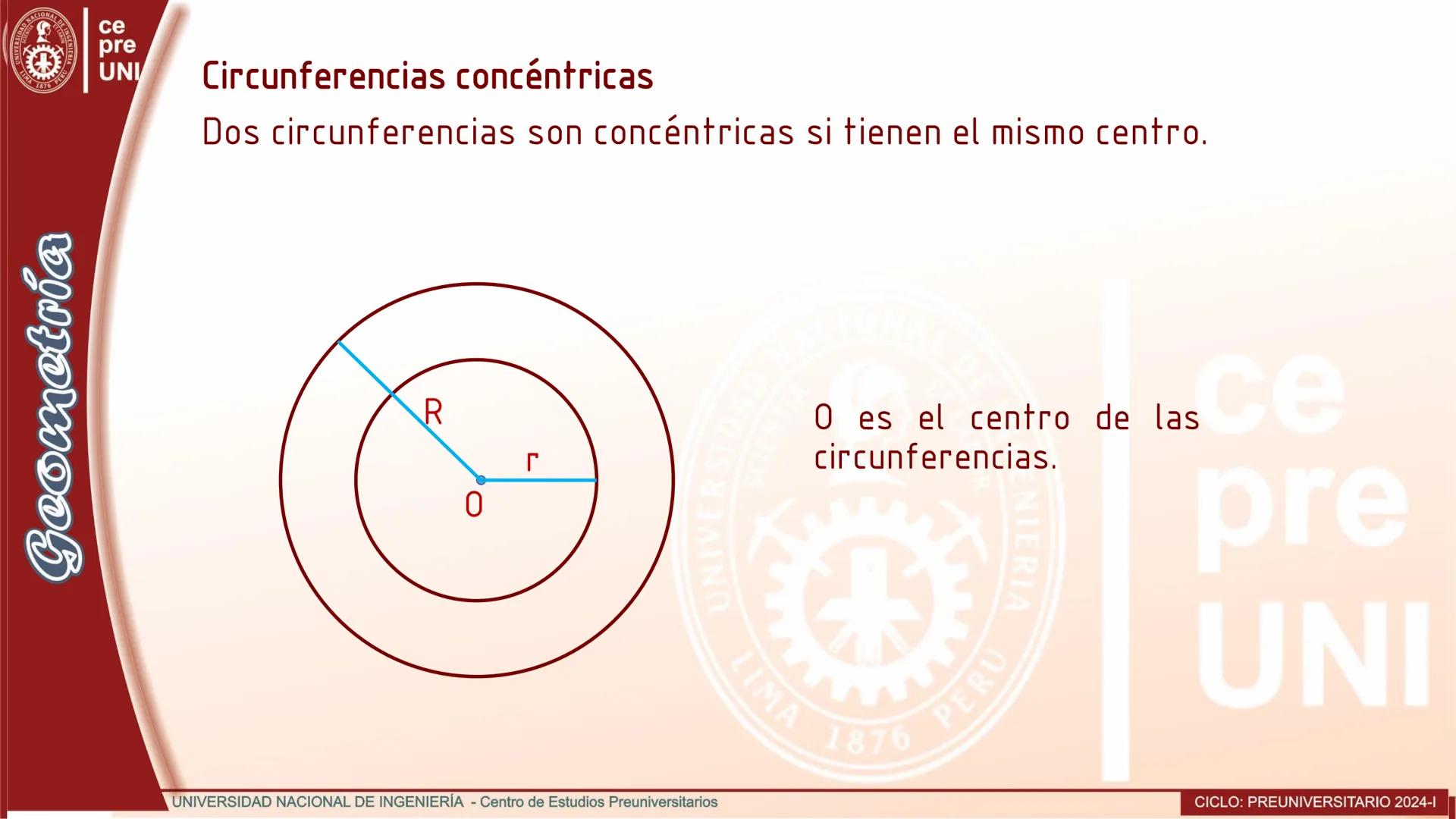
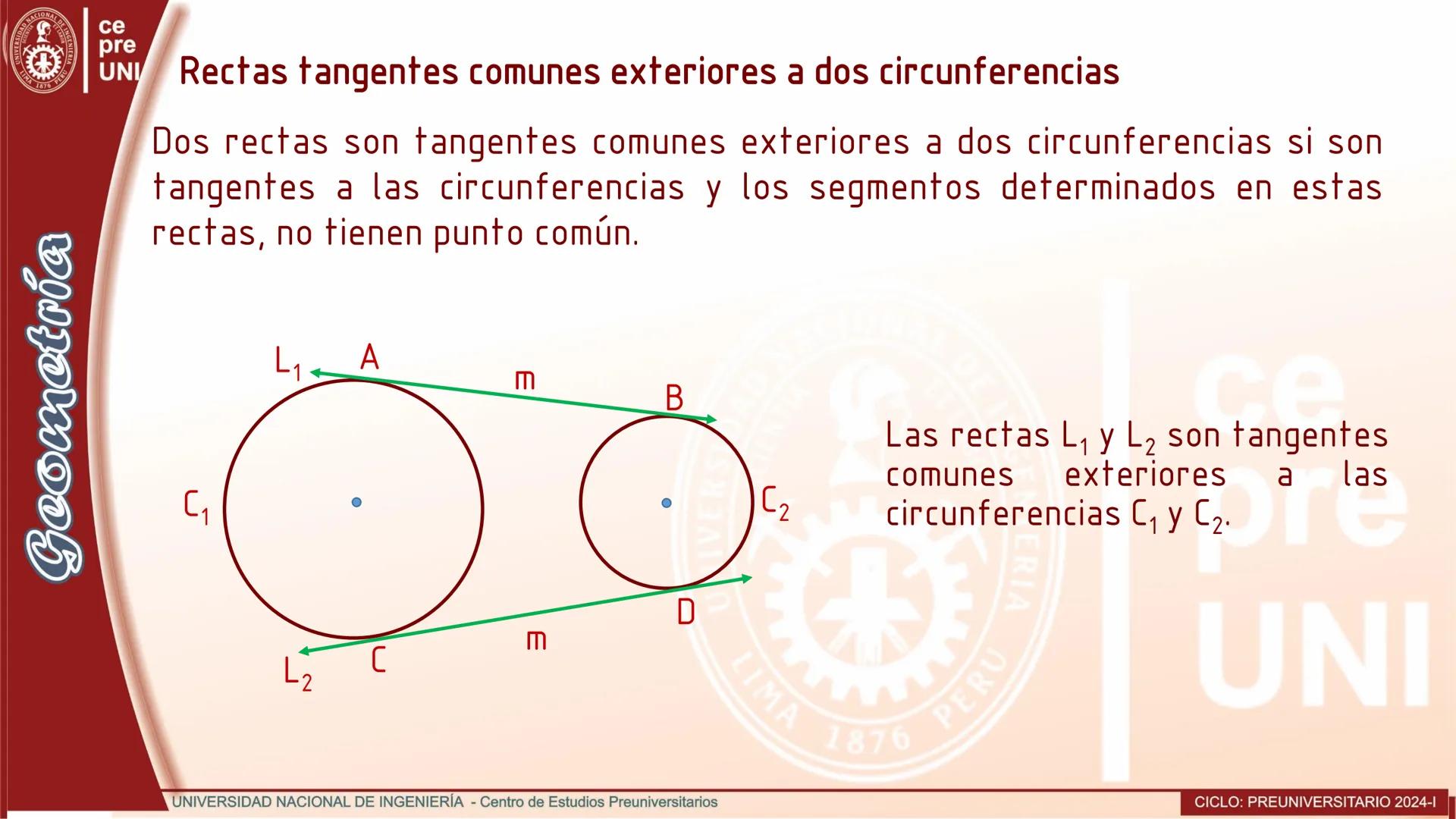
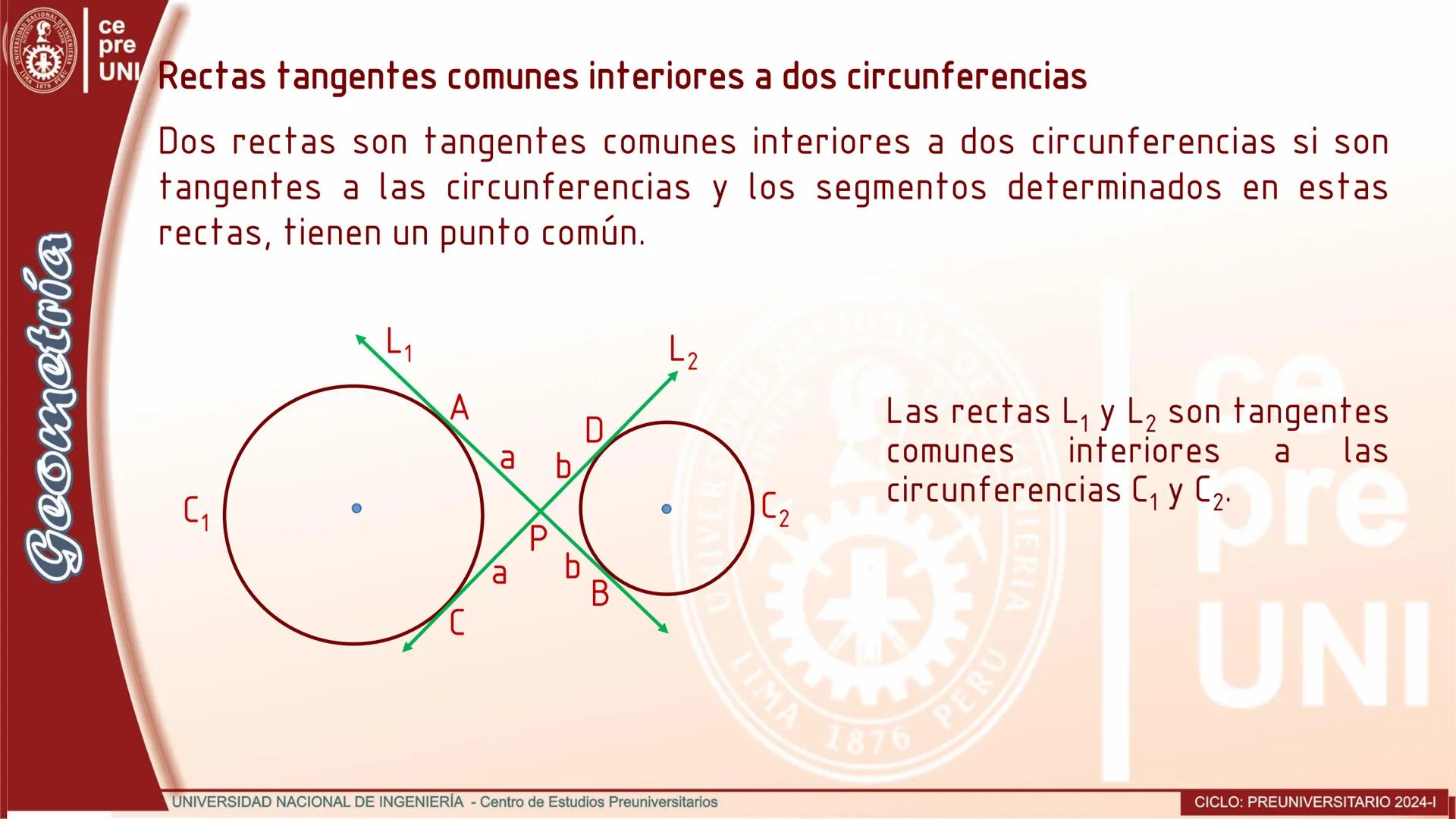
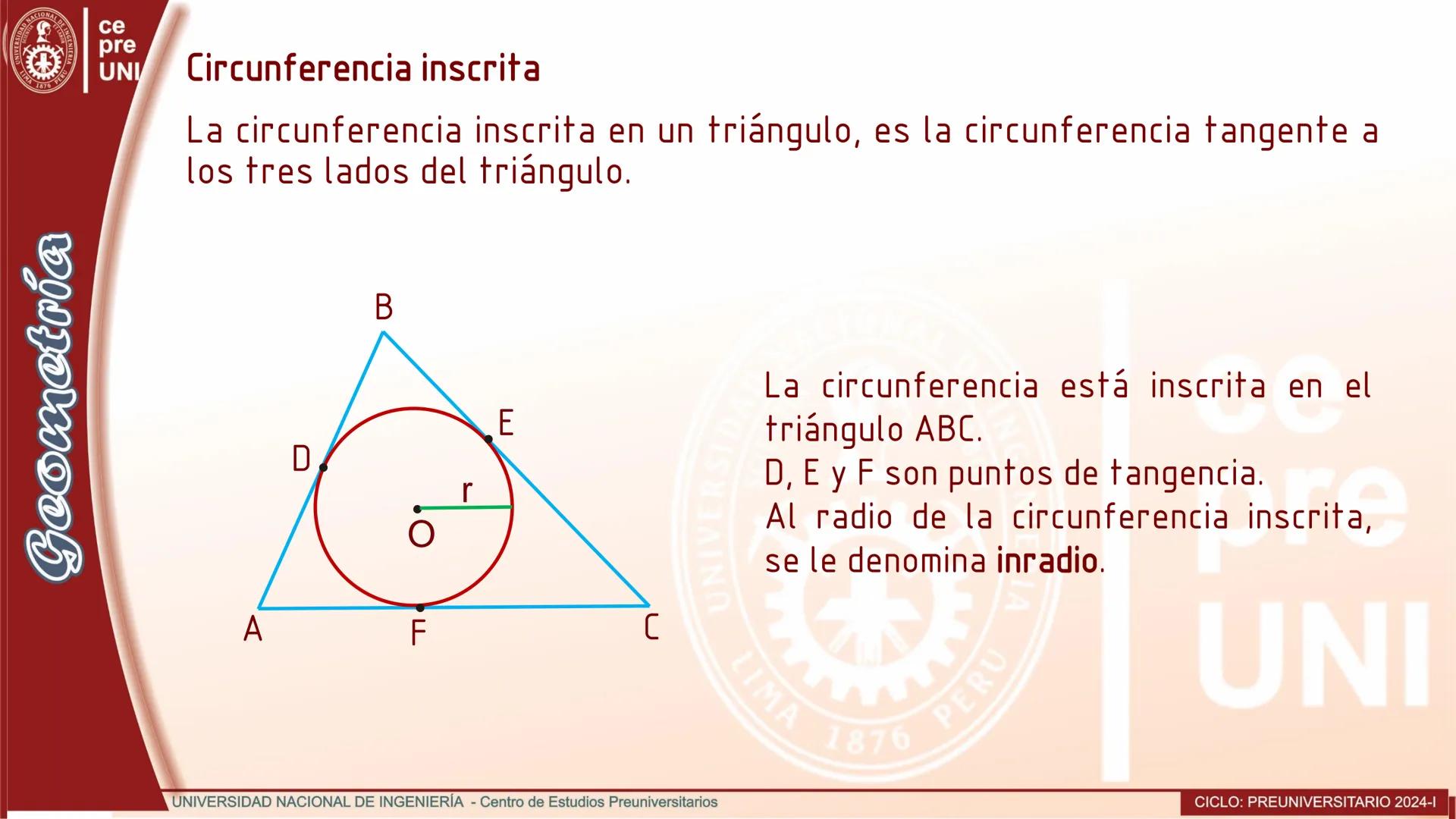
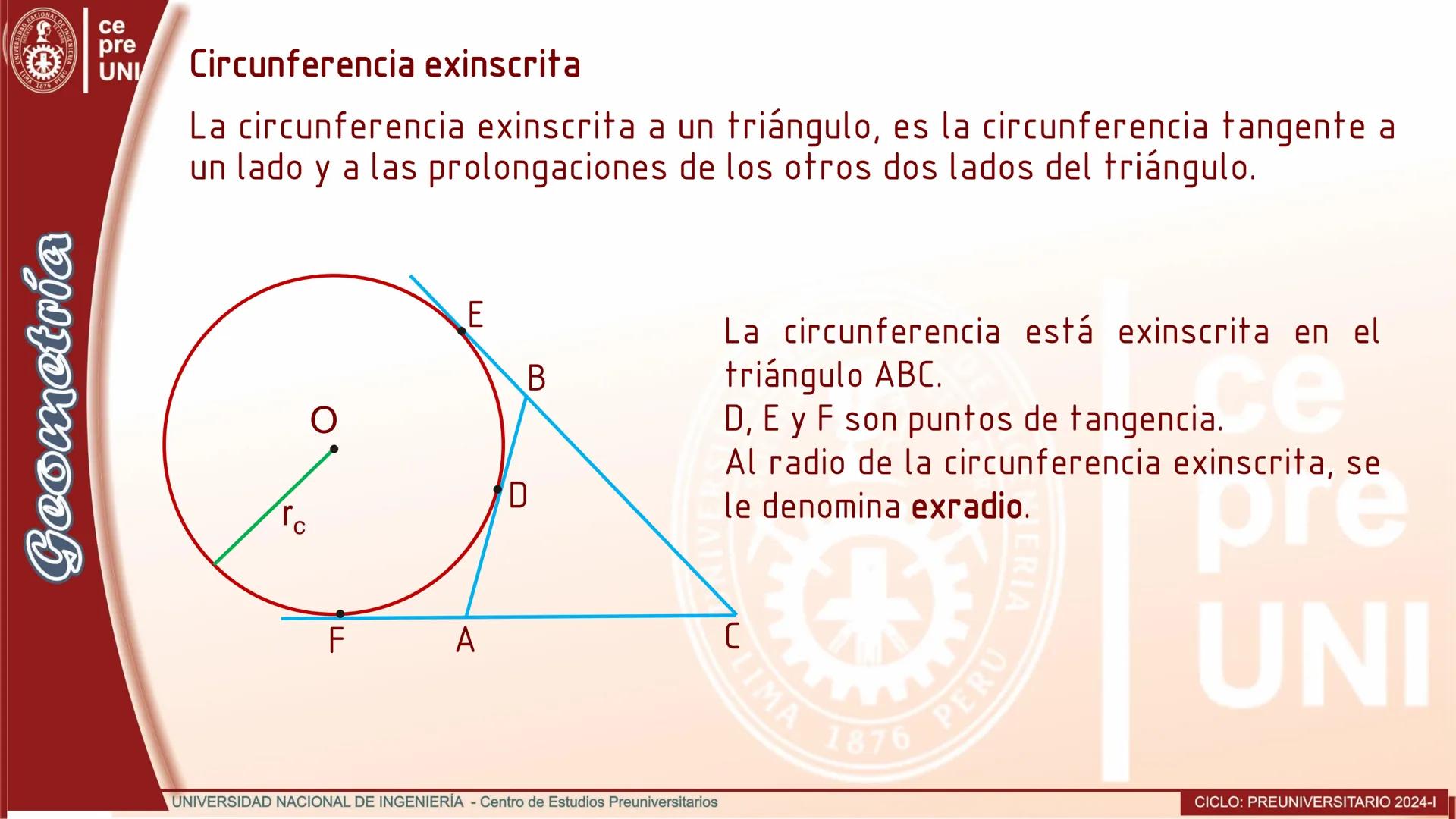
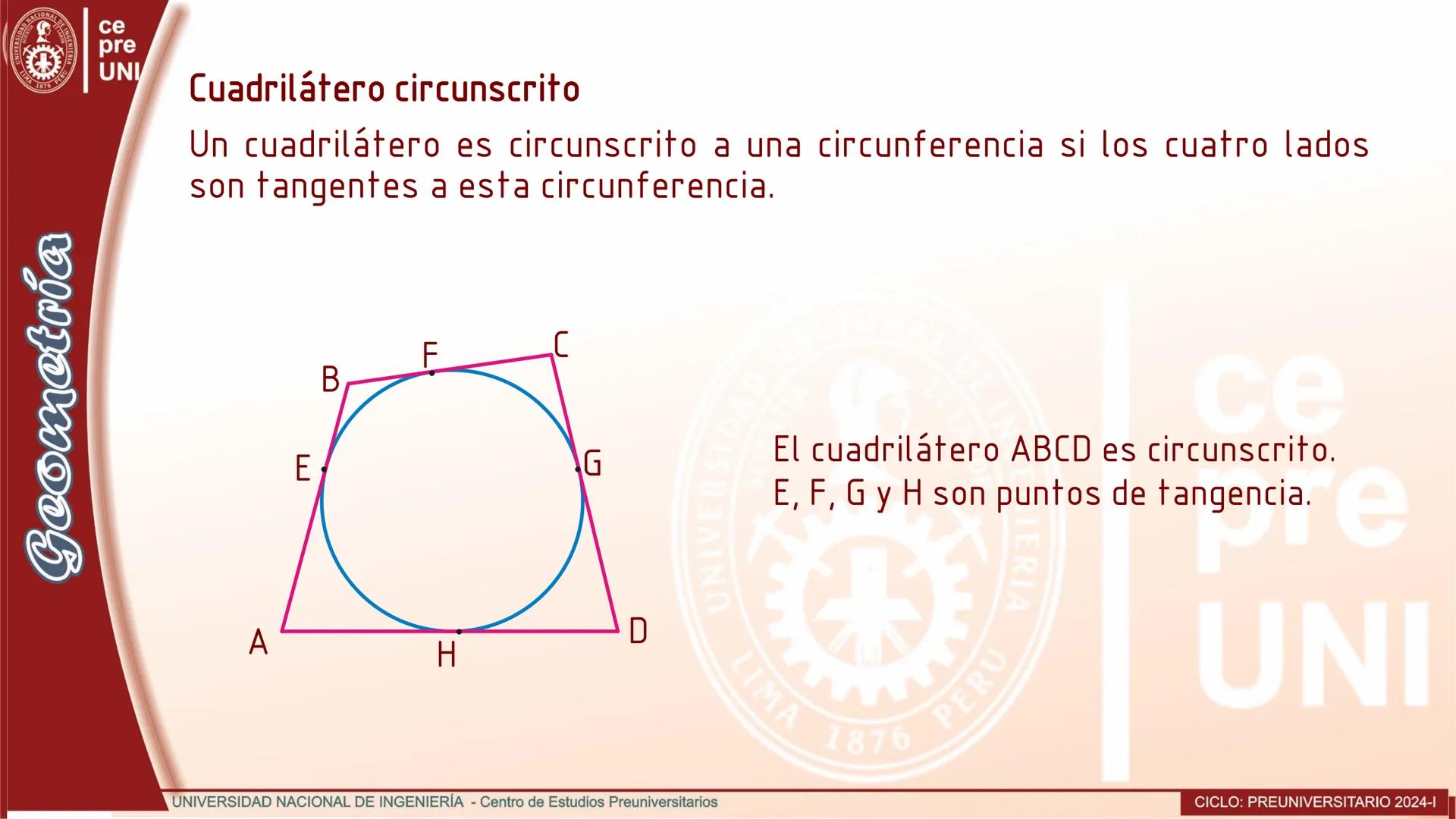
Cuerdas Paralelas y Arcos

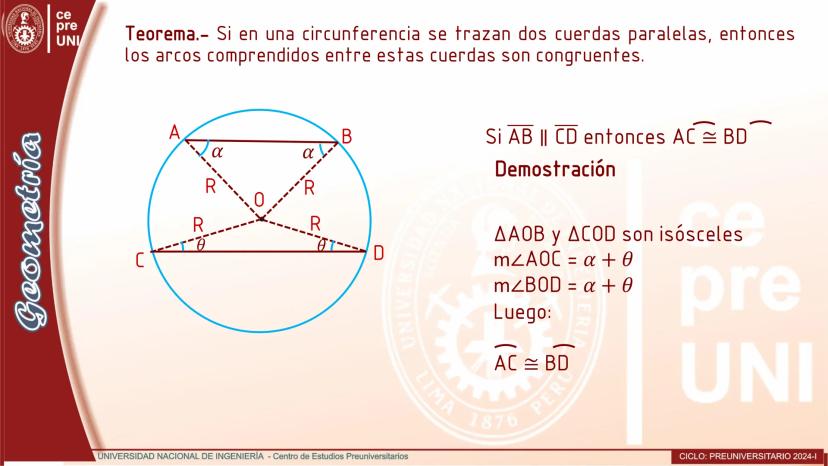
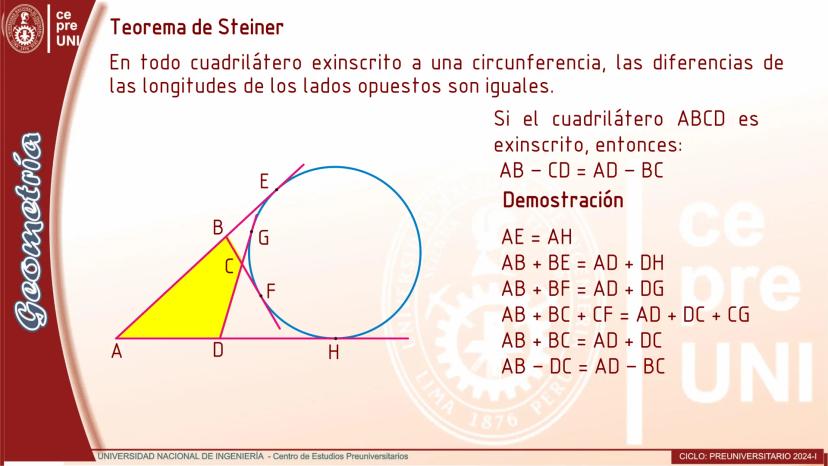
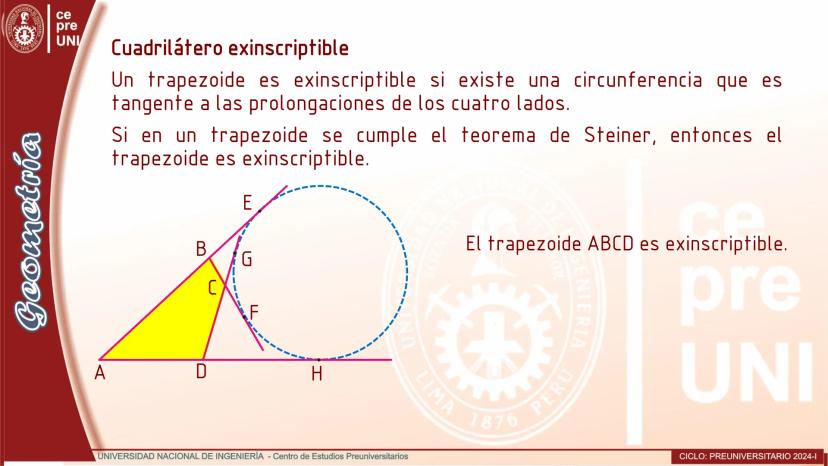
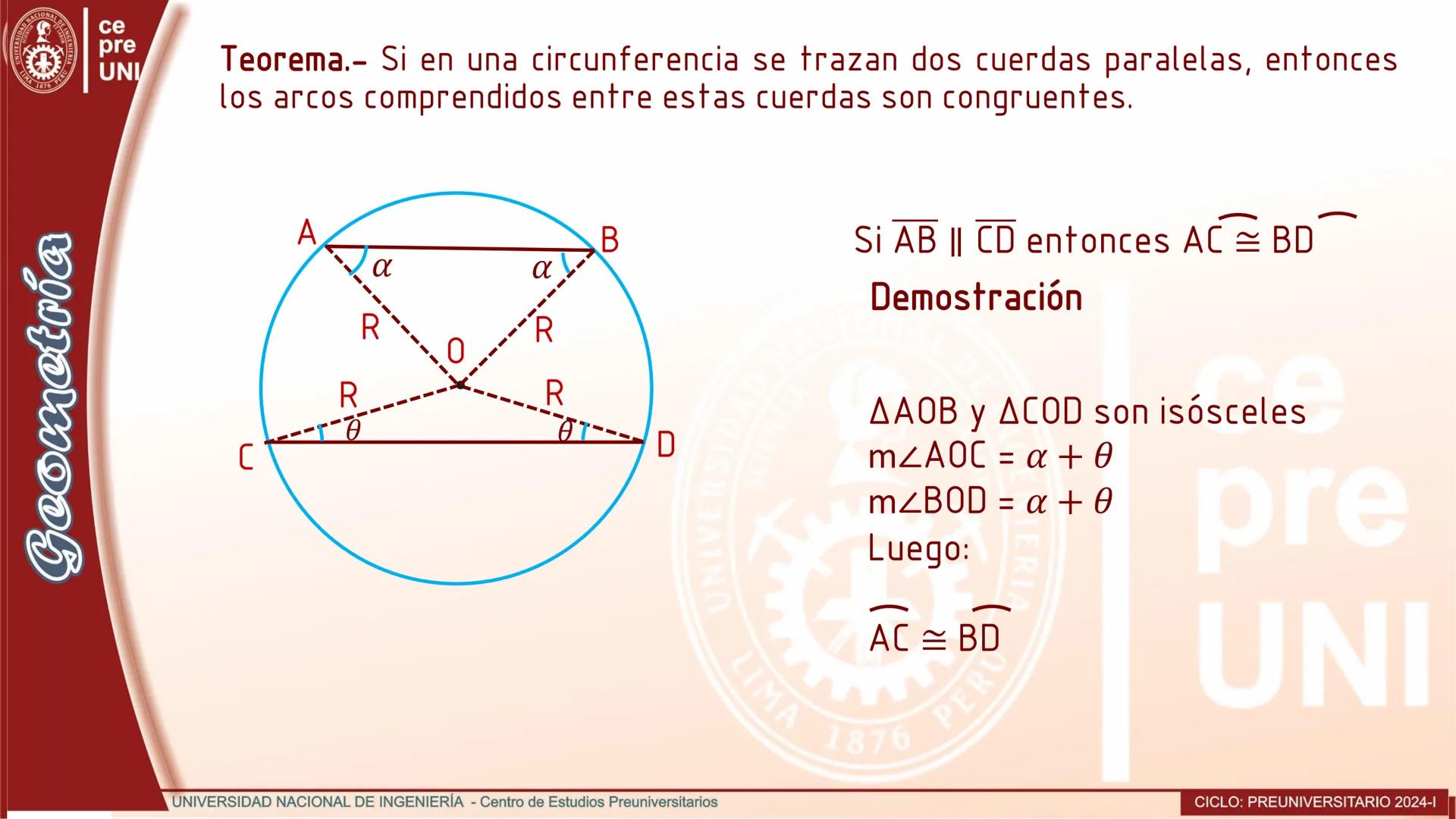
Cuando trazamos cuerdas paralelas en una circunferencia, se cumple el siguiente teorema: Si en una circunferencia se trazan dos cuerdas paralelas, entonces los arcos comprendidos entre estas cuerdas son congruentes.

Si AB y CD son cuerdas paralelas en una circunferencia, entonces los arcos AC y BD tienen exactamente la misma medida. Esto se debe a que los ángulos centrales que determinan estos arcos son iguales.

La demostración se basa en analizar los triángulos isósceles AOB y COD, donde encontramos que la medida del ángulo AOC es igual a la del ángulo BOD, lo que confirma que los arcos AC y BD son congruentes.

Esta propiedad es muy útil para resolver problemas que involucran construcciones geométricas con cuerdas paralelas o para determinar medidas de arcos en configuraciones específicas.