El círculo y sus partes son elementos fundamentales en geometría.... Mostrar más
Inscríbete para ver los apuntes¡Es gratis!
Acceso a todos los documentos
Mejora tus notas
Únete a millones de estudiantes
Al registrarte aceptas las Condiciones del servicio y la Política de privacidad.
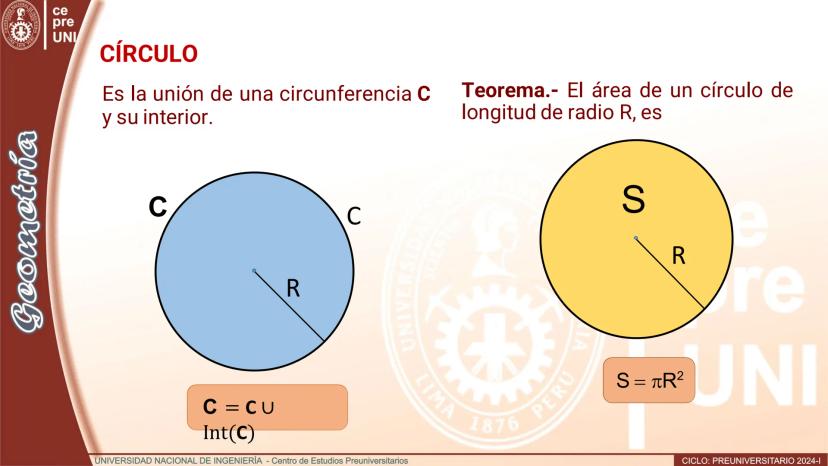

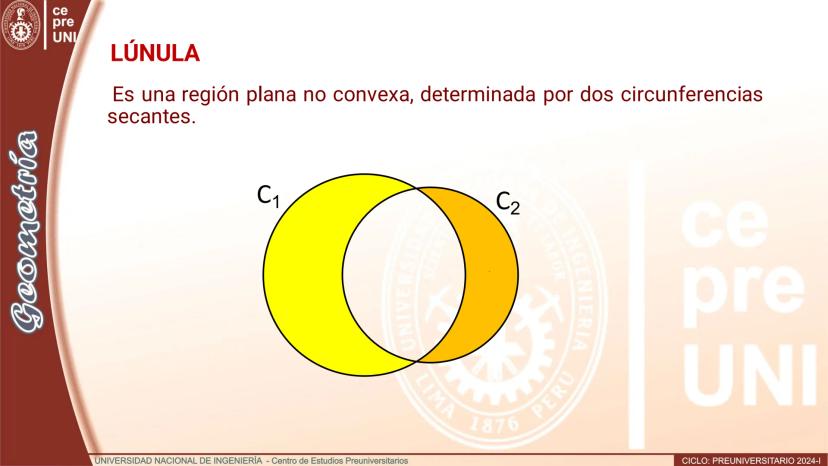
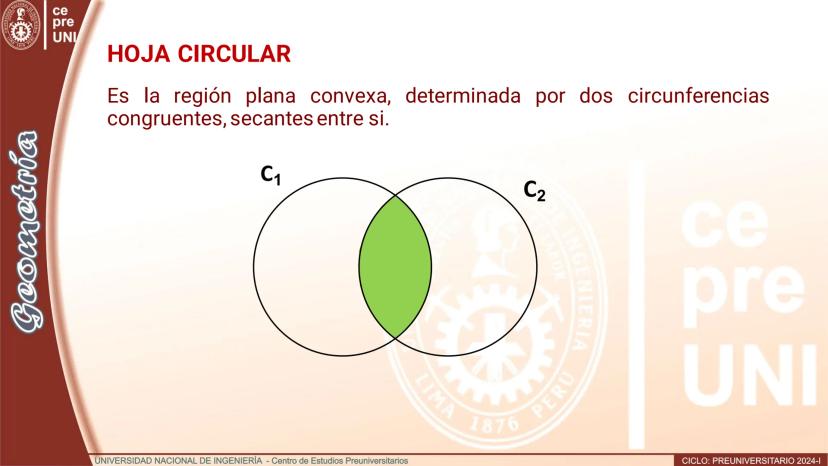
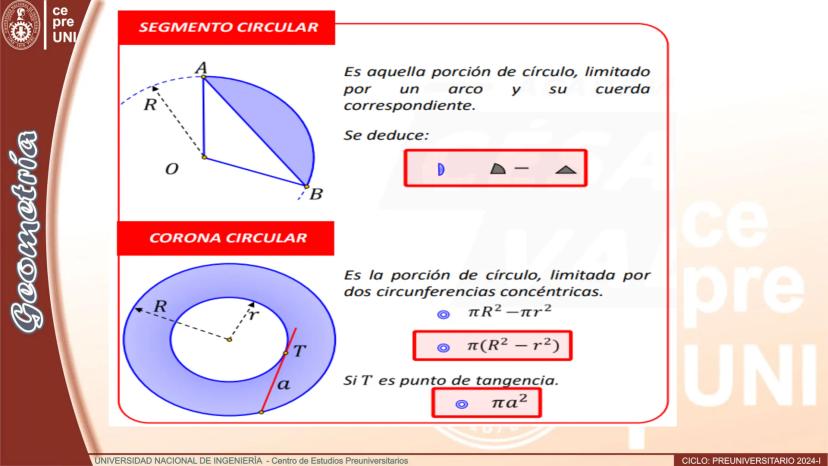
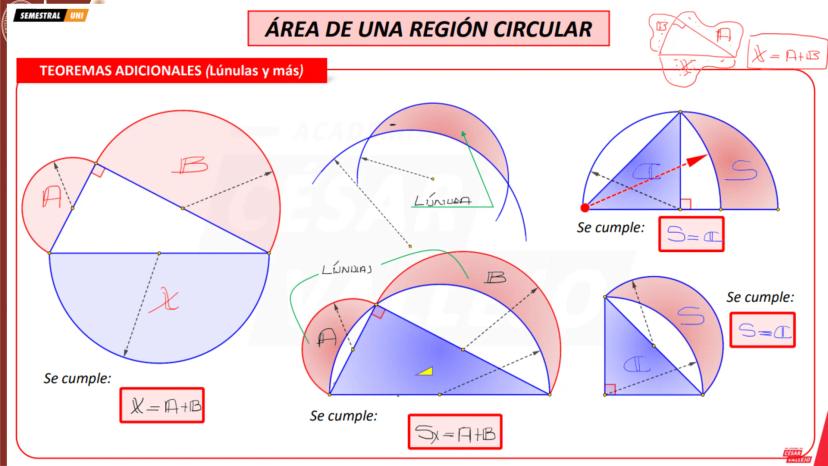


$C = C \cup Int(C)$
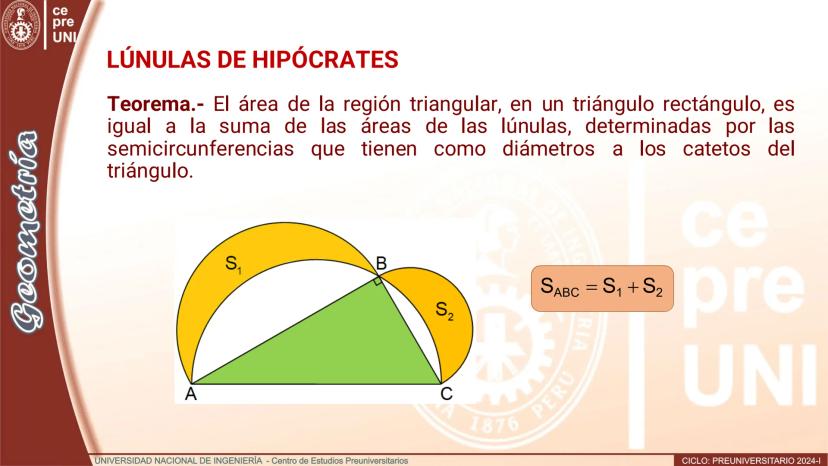
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_1.webp&w=2048&q=75)

$C = C \cup Int(C)$
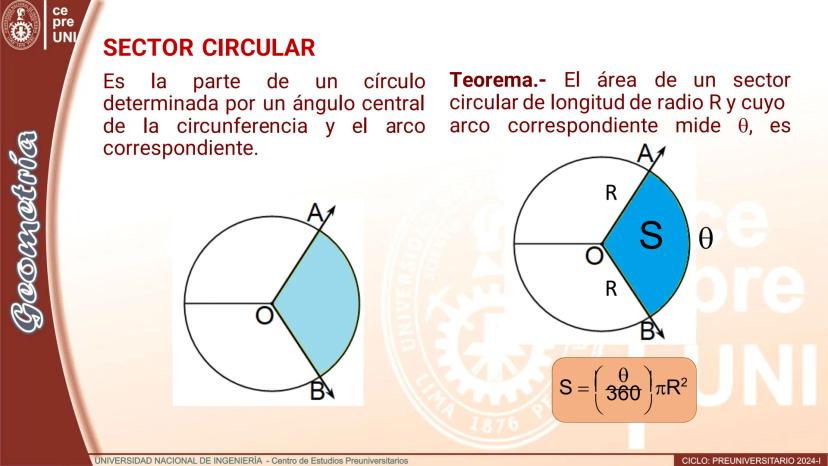
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_2.webp&w=2048&q=75)

$C = C \cup Int(C)$
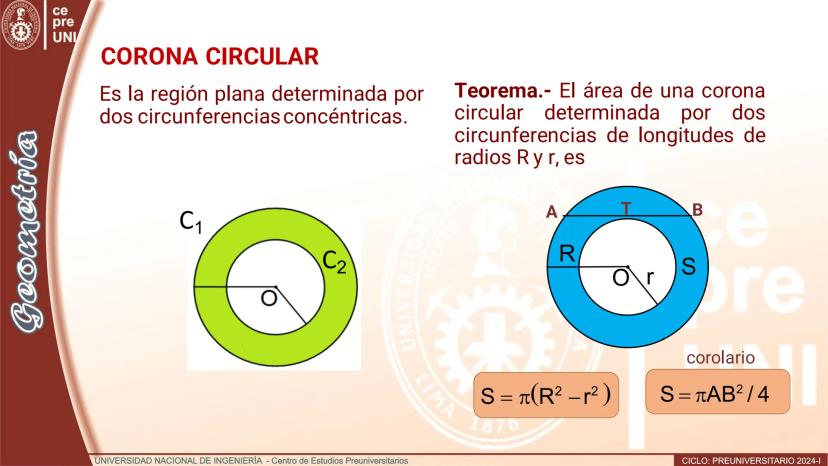
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_3.webp&w=2048&q=75)

$C = C \cup Int(C)$
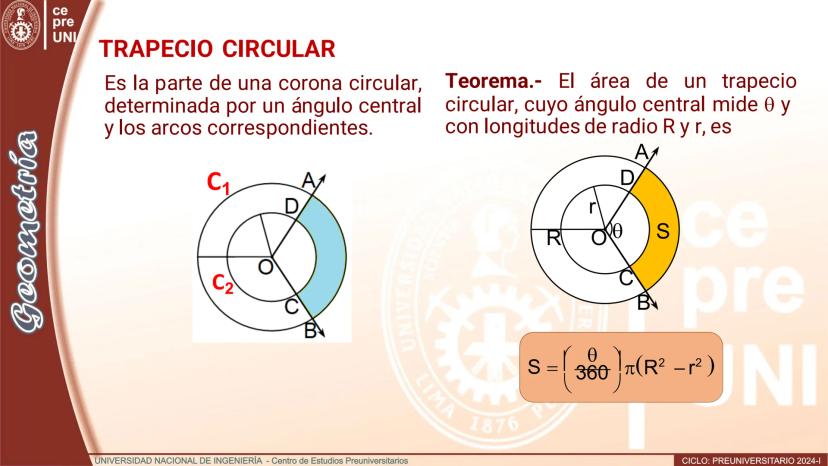
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_4.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_5.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_6.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_7.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_8.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_9.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_10.webp&w=2048&q=75)

$C = C \cup Int(C)$
Teorema.- El área de un](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F019783de-4f54-7ee3-8b3c-51836a6b2638_image_page_11.webp&w=2048&q=75)