Objetivos del Análisis Dimensional y Vectorial

La física se vuelve mucho más manejable cuando dominas dos conceptos clave. Primero, el análisis dimensional te permite verificar si tus ecuaciones están bien planteadas antes de hacer cálculos complicados. Segundo, los vectores te dan las herramientas para trabajar con magnitudes que tienen dirección y sentido.

Las fórmulas que ves como $F = ma$ o $v_f = v_0 + at$ no son solo números al azar. Cada una tiene una lógica dimensional que puedes verificar usando las reglas del análisis dimensional.

💡 Tip clave: Antes de resolver cualquier problema, siempre verifica que tu ecuación sea dimensionalmente correcta. Te ahorrará tiempo y errores.

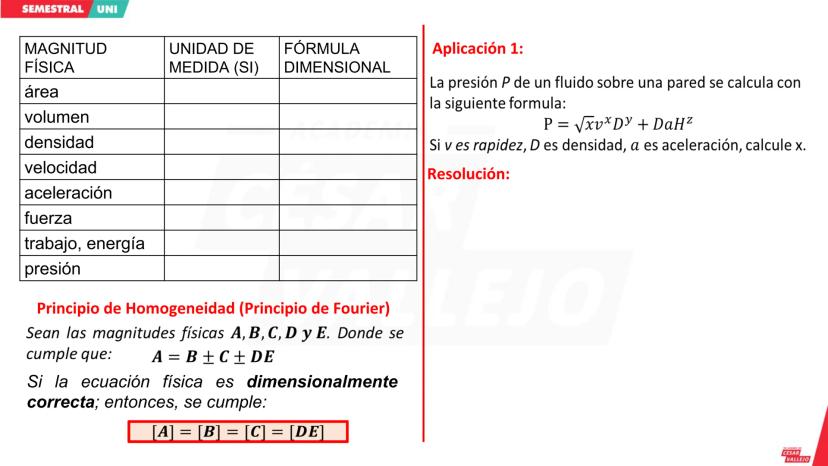
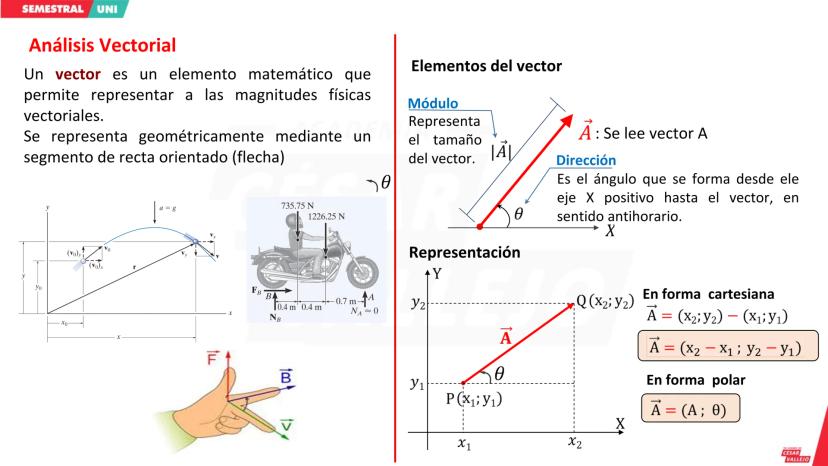
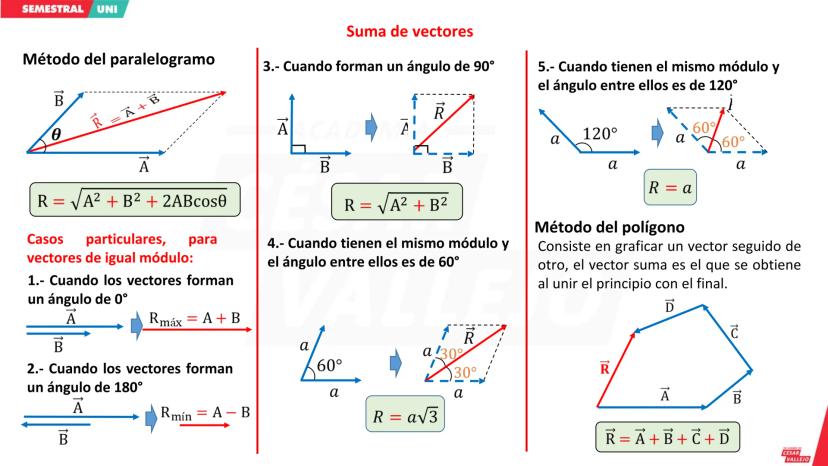
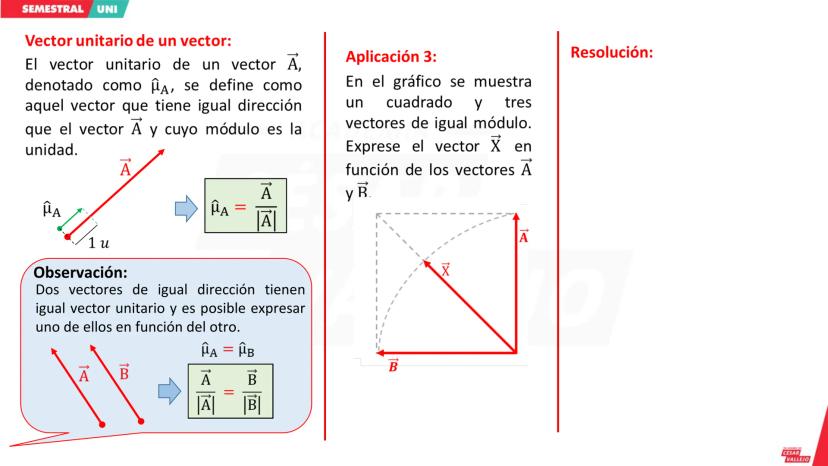
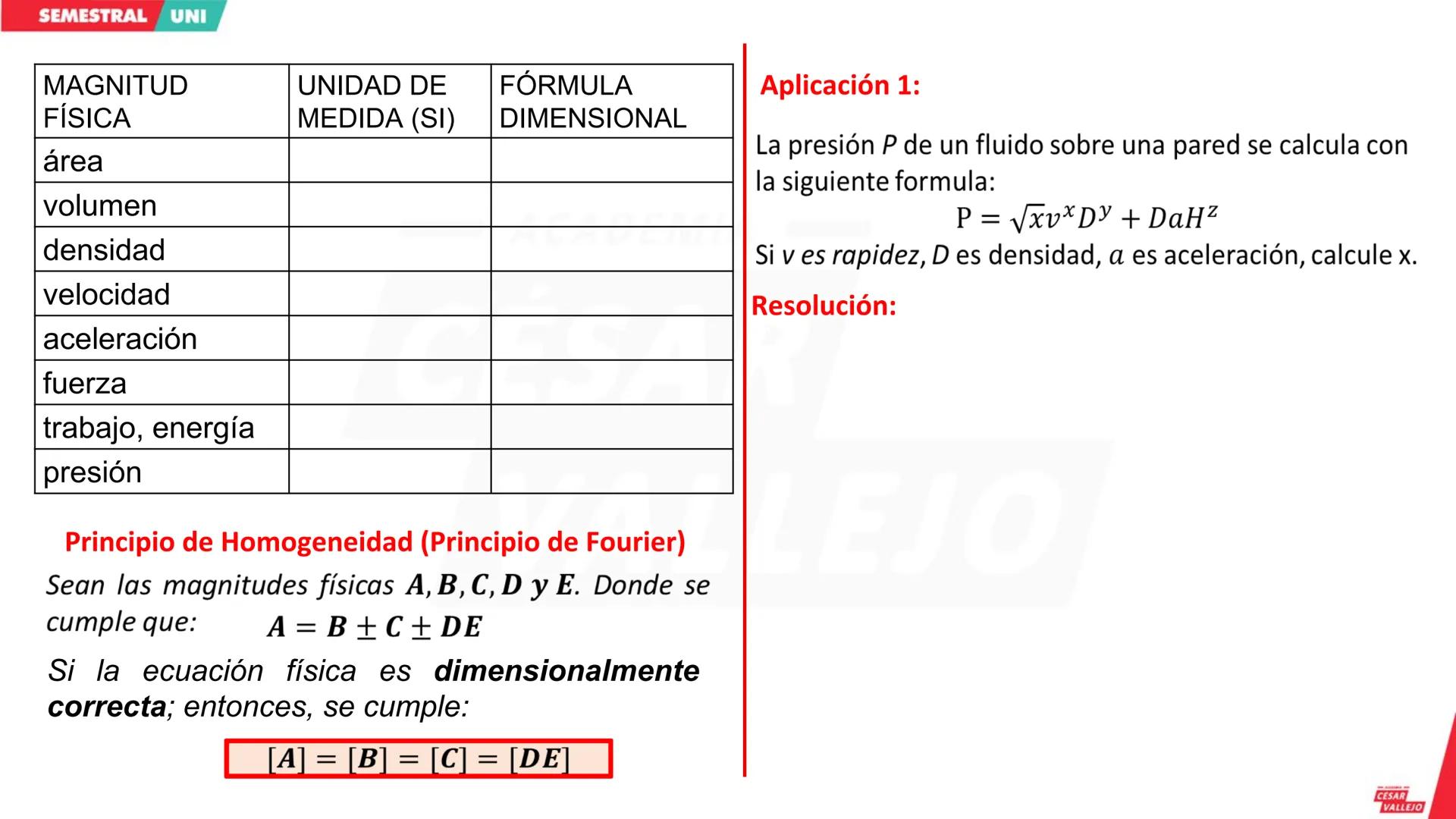
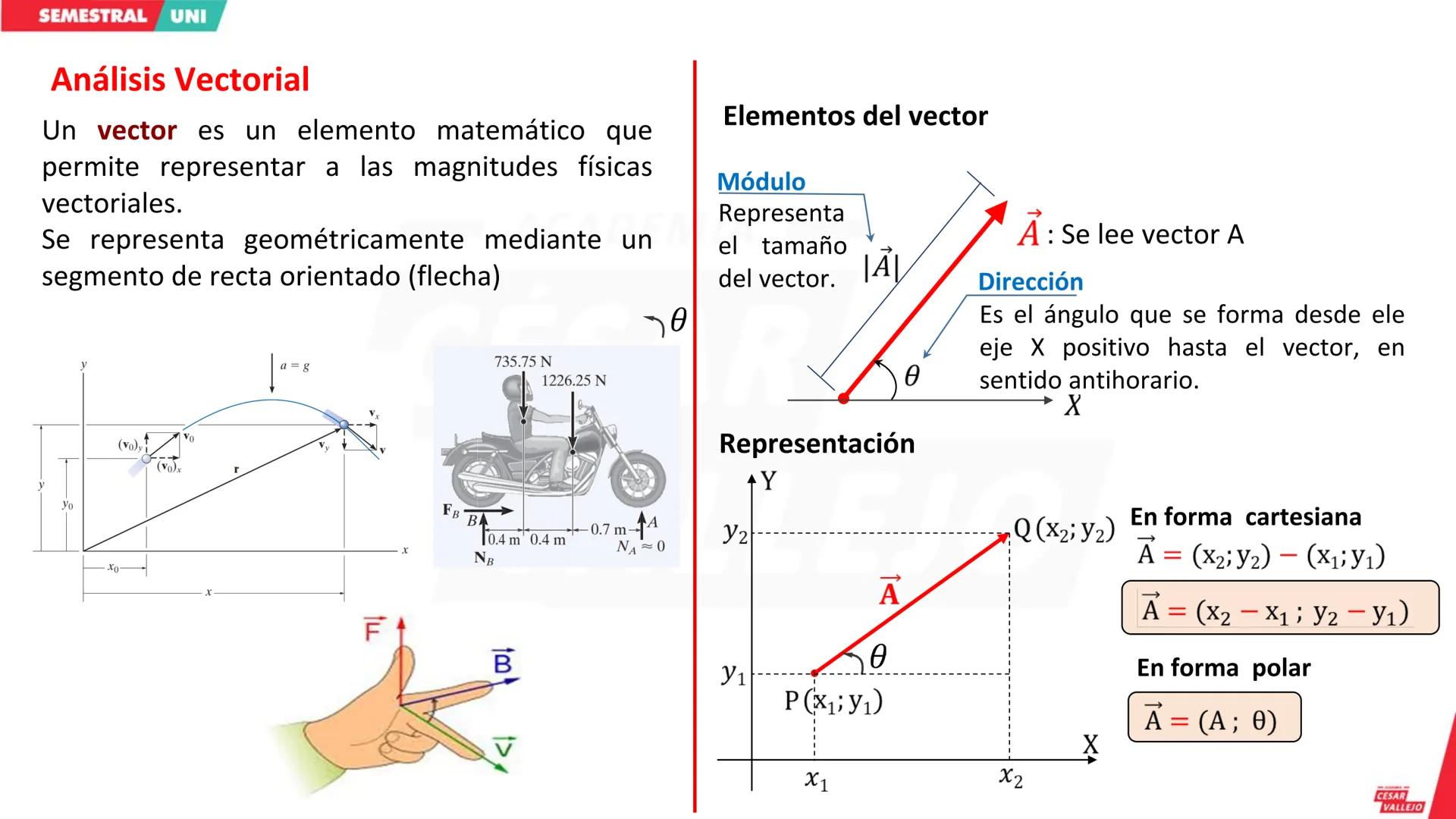
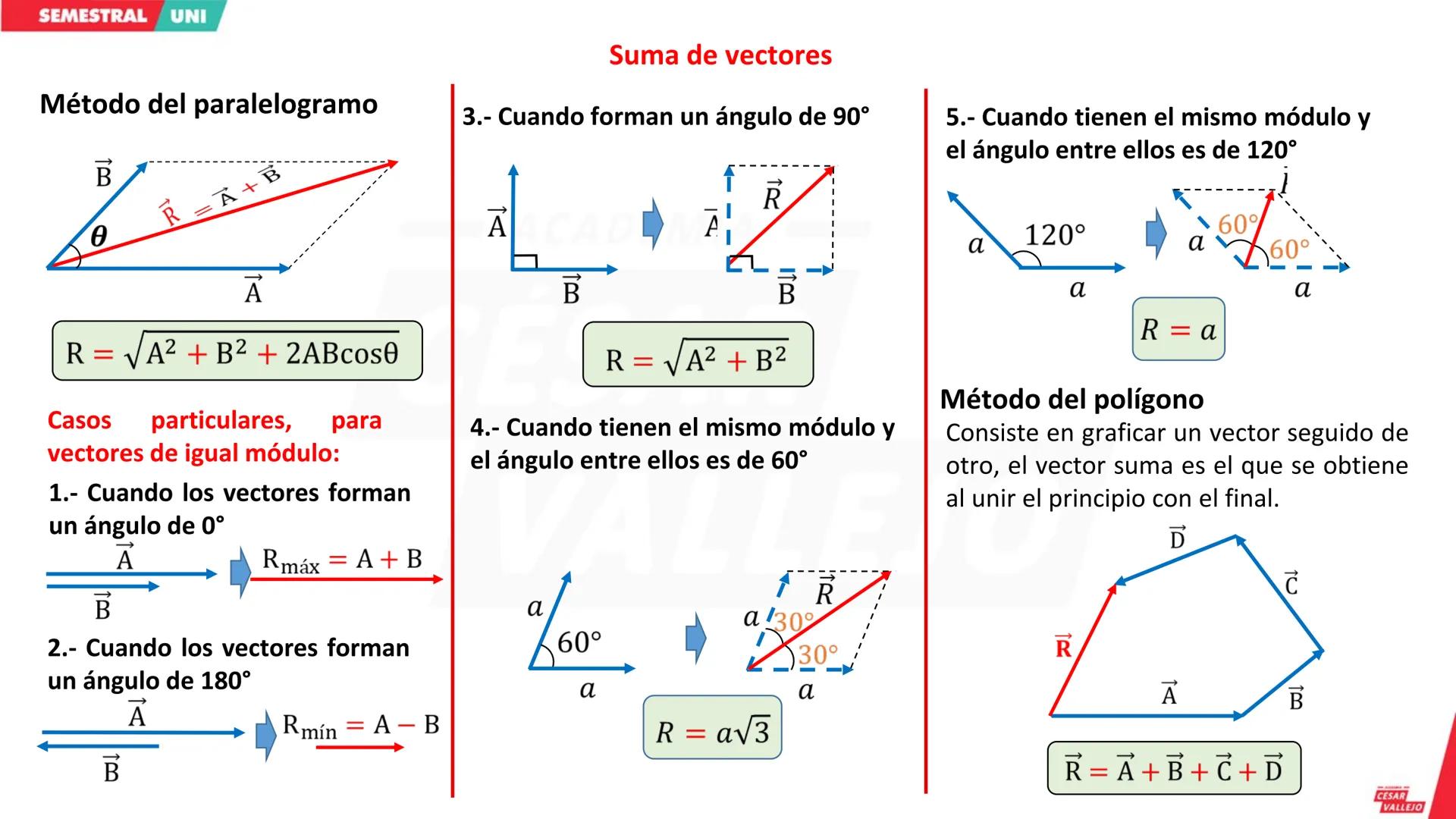
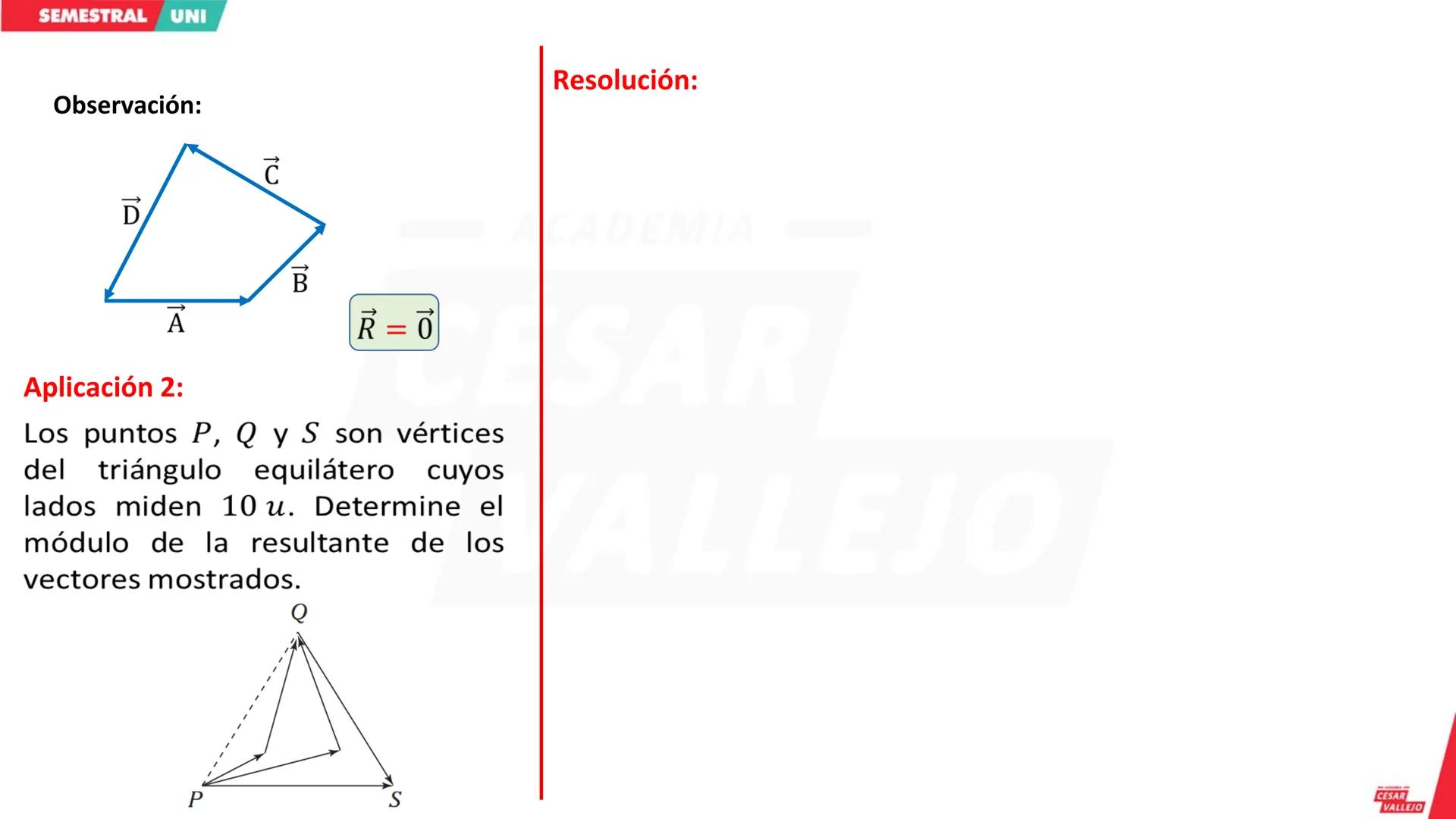
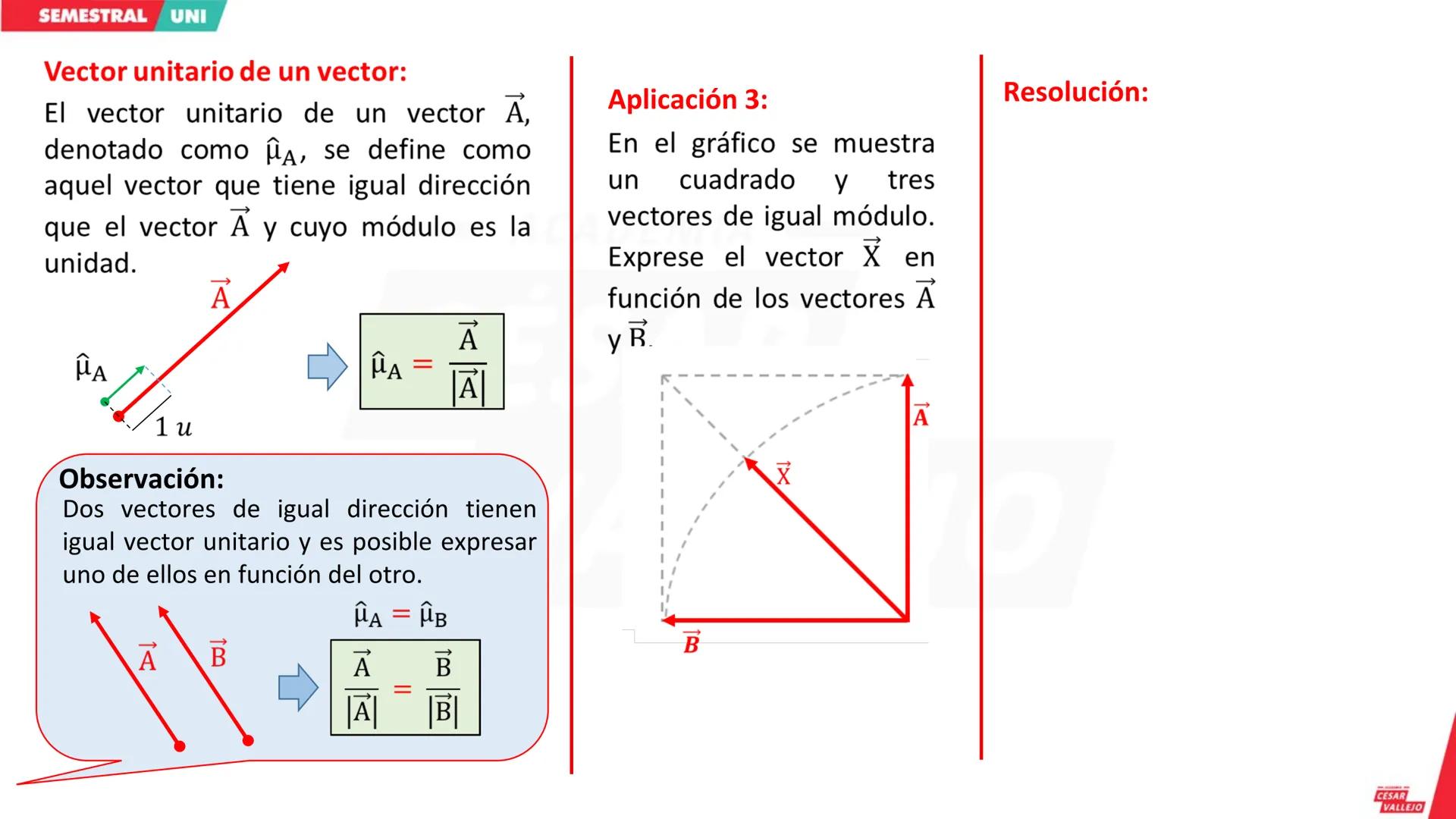
Conceptos Básicos del Análisis Dimensional

El análisis dimensional es como el "detective" de la física que investiga si las ecuaciones tienen sentido. Estudia cómo se relacionan las magnitudes fundamentales (longitud L, masa M, tiempo T) con las magnitudes derivadas.

Si tienes una magnitud física A, su fórmula dimensional se escribe como $A$. Las magnitudes fundamentales más importantes son longitud $L$, masa $M$, tiempo $T$, temperatura $θ$, intensidad de corriente $I$, intensidad luminosa $J$ y cantidad de sustancia $N$.

Las propiedades básicas son súper útiles: $AB$ = $A$$B$, $A/B$ = $A$/$B$, y $A^n$ = $A$^n. Algo importante: los números, funciones trigonométricas y logaritmos siempre tienen dimensión igual a 1.

💡 Recuerda: Los ángulos, senos, cosenos y números como π siempre son adimensionales ([π] = 1).

Principio de Homogeneidad y Aplicaciones

El Principio de Fourier es tu mejor aliado para verificar ecuaciones. Dice que si tienes A = B ± C ± DE, entonces $A$ = $B$ = $C$ = $DE$. Básicamente, solo puedes sumar o restar términos que tengan las mismas dimensiones.

Las magnitudes derivadas más comunes tienen fórmulas específicas: área $L²$, volumen $L³$, densidad $ML⁻³$, velocidad $LT⁻¹$, aceleración $LT⁻²$, fuerza $MLT⁻²$, y presión $ML⁻¹T⁻²$.

Para resolver problemas, identifica las magnitudes involucradas, aplica el principio de homogeneidad y despeja las incógnitas. Es como armar un rompecabezas donde las piezas deben encajar perfectamente.

💡 Estrategia: Siempre empieza identificando qué magnitudes físicas están involucradas en el problema.

Fundamentos del Análisis Vectorial

Un vector es mucho más que un número: representa magnitudes que tienen tanto tamaño como dirección. Piensa en la velocidad de un auto - no solo importa qué tan rápido va, sino hacia dónde se dirige.

Todo vector tiene dos elementos clave: el módulo (su tamaño, escrito como |Ā|) y la dirección (el ángulo que forma con el eje X positivo, medido en sentido antihorario).

Puedes representar vectores de dos formas principales. En forma cartesiana: Ā = $x₂ - x₁; y₂ - y₁$, que te dice cuánto se mueve en cada eje. En forma polar: Ā = (A; θ), donde A es el módulo y θ es el ángulo.

💡 Visualiza: Siempre dibuja los vectores como flechas. Te ayudará a entender mejor las operaciones.

Métodos de Suma de Vectores

La suma de vectores tiene reglas específicas que debes dominar. El método del paralelogramo usa la fórmula R = √$A² + B² + 2AB cos θ$, donde θ es el ángulo entre los vectores.

Los casos especiales son súper útiles para exámenes: cuando θ = 0°, R_max = A + B; cuando θ = 180°, R_min = A - B; cuando θ = 90°, R = √$A² + B²$. Para vectores iguales con θ = 60°, R = a√3, y con θ = 120°, R = a.

El método del polígono es más directo: colocas los vectores uno después del otro, y el vector resultante va desde el inicio del primero hasta el final del último. Es como seguir un mapa con varias direcciones.

💡 Truco: Para vectores perpendiculares, siempre usa Pitágoras. Es el caso más común en exámenes.

Aplicaciones Prácticas de Suma Vectorial

Cuando resuelves problemas con triángulos equiláteros o figuras geométricas, la clave está en identificar las simetrías. En un triángulo equilátero con lados de 10 u, los vectores suelen cancelarse parcialmente debido a la geometría.

La resultante nula $R = 0$ ocurre cuando los vectores se balancean perfectamente. Esto pasa frecuentemente en sistemas en equilibrio o cuando tienes vectores distribuidos simétricamente.

Para resolver estos problemas, descompone cada vector en sus componentes X e Y, suma algebraicamente las componentes, y luego calcula el módulo de la resultante.

💡 Observación: En figuras simétricas, muchas componentes se cancelan. Aprovecha esta propiedad.

Vectores Unitarios y Descomposición

Un vector unitario μₐ tiene la misma dirección que el vector original A, pero su módulo es exactamente 1. Es súper útil para indicar direcciones sin preocuparse por el tamaño.

Cuando dos vectores tienen la misma dirección, comparten el mismo vector unitario. Esto te permite expresar un vector en función del otro: si A y B tienen la misma dirección, entonces A/|A| = B/|B|.

Los vectores unitarios fundamentales son î (dirección X), ĵ (dirección Y) y k̂ (dirección Z), todos con módulo 1. Cualquier vector se puede escribir como combinación de estos.

💡 Aplicación: Los vectores unitarios son ideales para expresar direcciones en problemas de geometría.

Descomposición Rectangular de Vectores

La descomposición rectangular convierte cualquier vector en sus componentes perpendiculares. Para un vector A con ángulo θ: Aₓ = A cos θ y Aᵧ = A sen θ.

En el sistema tridimensional, cualquier vector se expresa como A = Aₓî + Aᵧĵ + Aᵢk̂, donde î, ĵ y k̂ son los vectores unitarios con |î| = |ĵ| = |k̂| = 1.

La notación de componentes A = (Aₓ; Aᵧ; Aᵢ) es más compacta y práctica para cálculos. Por ejemplo, A = (4; 3; 0) significa 4 unidades en X, 3 en Y y 0 en Z.

💡 Consejo: Siempre verifica que A² = Aₓ² + Aᵧ² + Aᵢ² para confirmar tu descomposición.

Producto Escalar de Vectores

El producto escalar (también llamado producto punto) toma dos vectores y produce un número. Para A⃗ · B⃗ = AₓBₓ + AᵧBᵧ + AᵢBᵢ, o usando la fórmula A⃗ · B⃗ = |A⃗| |B⃗| cos θ.

Este producto es especialmente útil para encontrar ángulos entre vectores o verificar si son perpendiculares $si A⃗ · B⃗ = 0, entonces θ = 90°$.

Cuando los vectores forman un polígono cerrado, su suma vectorial es cero. Esta propiedad te permite encontrar vectores desconocidos cuando conoces los otros del sistema.

💡 Aplicación: El producto escalar aparece en trabajo mecánico: W = F⃗ · d⃗.