Diagonales medias desde lados consecutivos
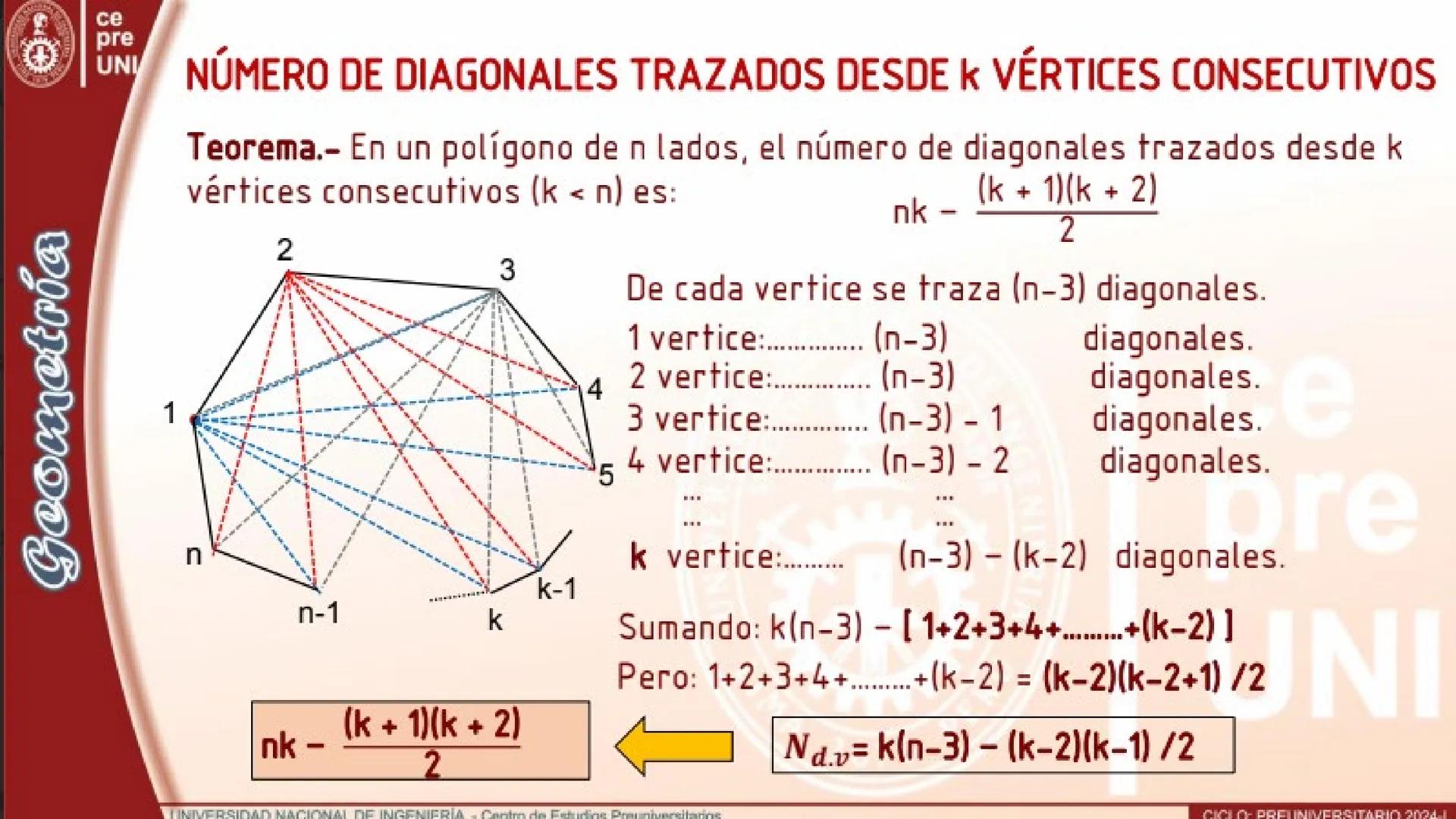
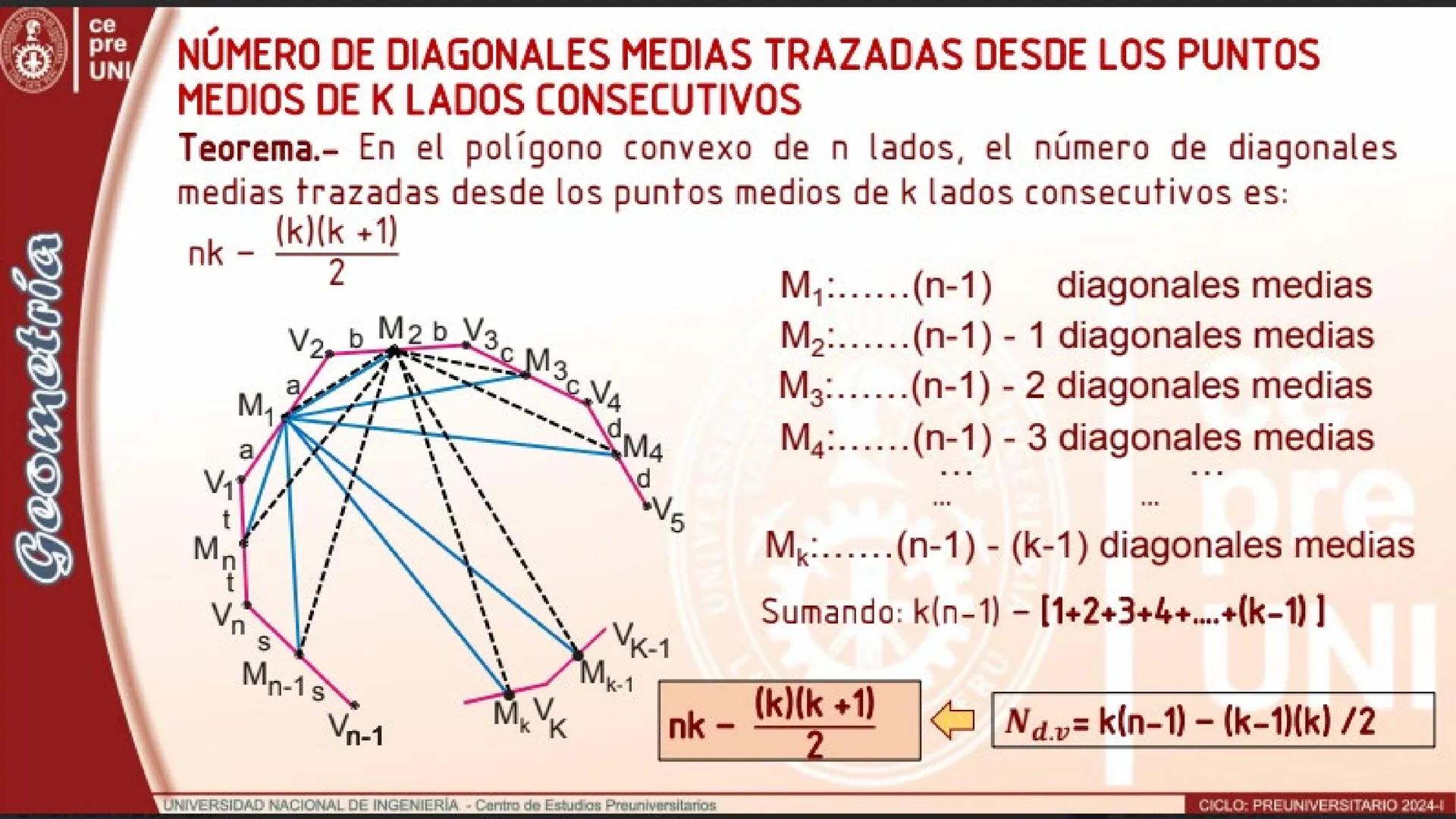
Cuando trabajas con diagonales medias desde k lados consecutivos, usas la fórmula: nk - kk+1/2. El patrón es similar a los vértices consecutivos, pero con una diferencia clave.
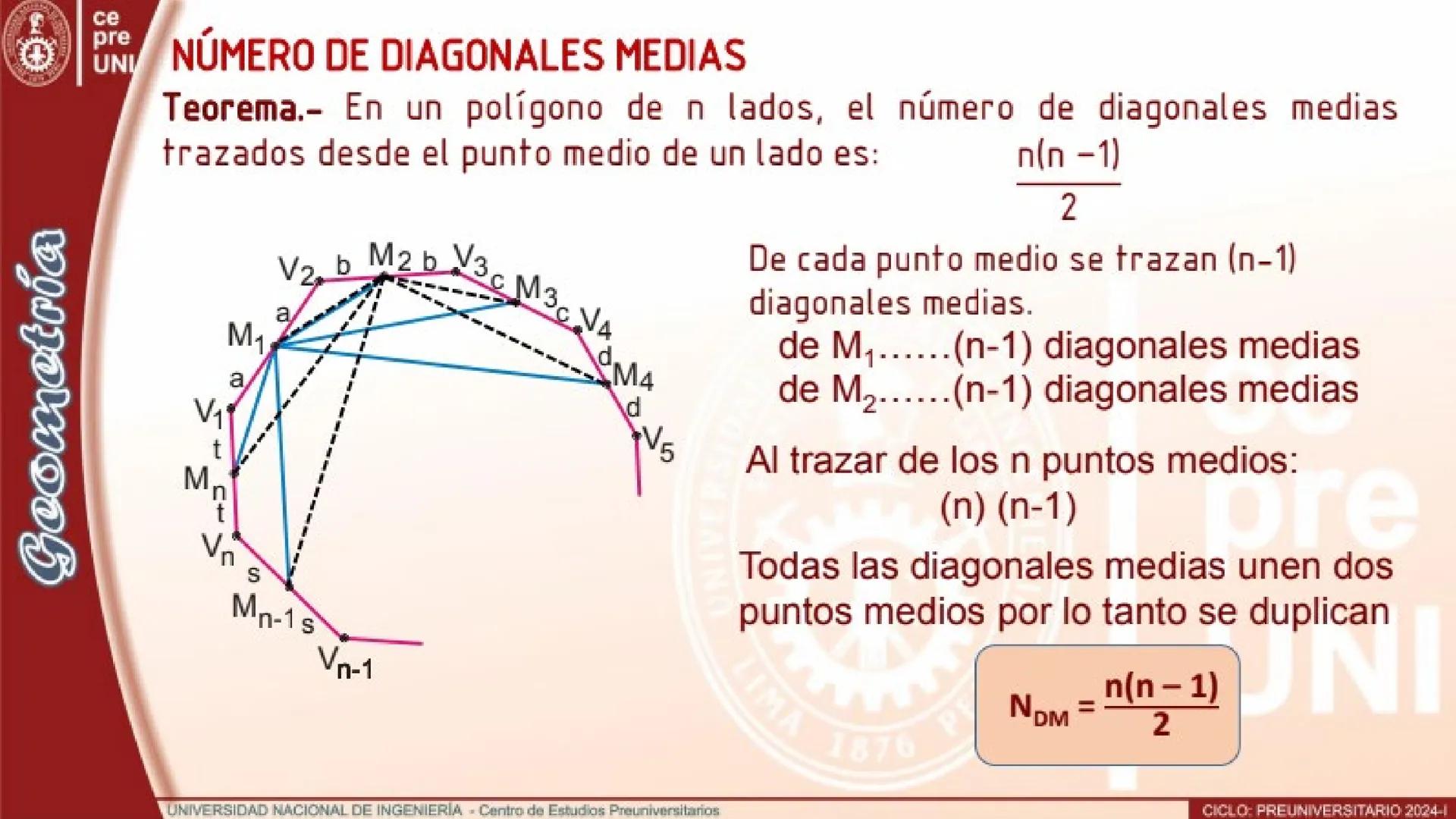
Aquí, el primer punto medio traza n−1 diagonales medias, el segundo traza n−1-1, el tercero traza n−1-2, y así sucesivamente. La reducción es porque van perdiendo conexiones con los puntos medios anteriores.
La suma total es kn−1 menos la suma 1+2+3+...+k−1, que igual a kk−1/2. Simplificando, obtienes nk - kk+1/2.
Patrón importante: En ambos tipos de diagonales consecutivas, siempre restas una progresión aritmética.